Question
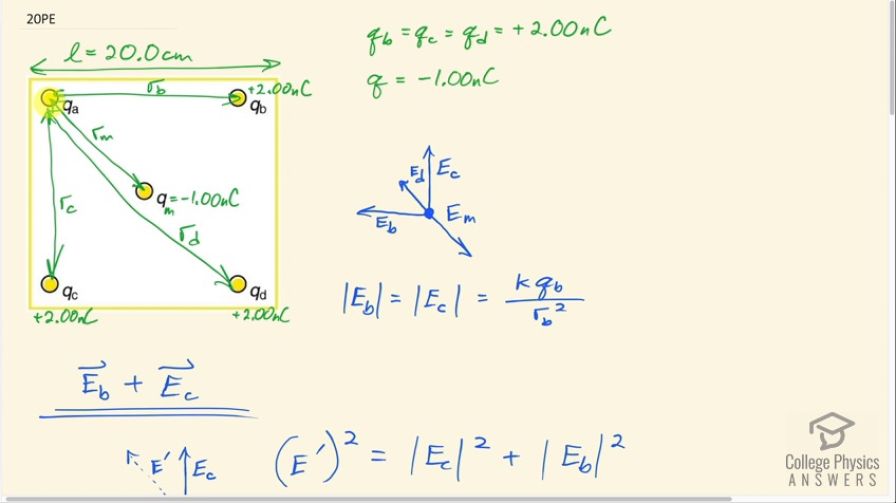
Find the electric field at the location of qa in Figure 18.52 given that , , and the square is 20.0 cm on a side.
Final Answer
above the x-axis to the left.
Solution video
OpenStax College Physics for AP® Courses, Chapter 18, Problem 20 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. We are going to find the electric field at this position here in this corner that's labeled q a but there's no actual charge here; there is a charge in the middle with a magnitude of 1.00 nanocoulomb and it's negatively charged. In the other three corners, there are charges of positive 2.00 nanocoulombs. So the electric field will be pointing upwards due to charge c because it would repel a test charge that is here and charge b would make an electric field straight to the left because it would repel to the left any positive test charge placed here. This charge way on the diagonal, charge d, will repel but its magnitude of its repulsion will be less than that of charge b or c since it's further away and charge m in the middle is going to have an electric field straight towards the middle because it's negatively charged and it would attract any positive test charge here and the magnitude of the field due to charge m will be twice that of charge d because even though this charge is half as big— 1 is half of 2— its distance is half as much and so you know if you have some charge or some electric field 1 which is kq 1 over r 1 squared and some other field number 2 kq 2 over r 2 squared. If q 2 is half of q 1, this would be like in the middle— like q 2 would be the middle charge but also half of the distance of the first charge— this works out to one-half over one-quarter which in total is 2 times kq 1 over r 1 squared. Okay! So just to illustrate that when you take half the charge and half the distance, you end up with 2 times the field strength. Okay so this vector is meant to be twice as long as this one. So these two vectors are in opposite directions but they are collinear so they are both 45 degrees with respect to horizontal and this vector E c and this vector E b are at right angles to each other and the resultant of these two will be along this diagonal here 45 degrees above the horizontal to the left. So if we can find the resultant of E c and E b— and that will be some vector like this— we'll call it E prime and then we'll have three vectors that are collinear that we can just add and subtract like scalars since they are along the same line; this one will be negative say and then these two will be positive. So that's gonna be our strategy: first we are gonna figure out what is E b plus E c and so we will find that resultant and then we will add to that E d and subtract from that E m. So E prime is the resultant of E c and E b and its square is going to be the square of E c— which is entirely vertical—squared plus the magnitude of E b—which is entirely horizontal—squared. So E c and E b make the vertical and horizontal components of this E prime and since these are of equal magnitude, we can say that this is going to be 2 times one of them squared because E c and E b are of equal charge and equal distance which is a side length of the square away from this point. So that means E prime then has a magnitude of the square root of all that which is square root 2 times E b. So that's square root 2 times kq b over r b squared because that's what the magnitude of E b is and r b is the distance from b to this point. Okay! r b is l because it's the side length of the square so we substitute in l here and we get E prime then is square root 2 times kq b over l squared and it's directed 45 degrees above the x-axis to the left and we can tell that by this triangle here where you have a triangle with legs that are equal and it's a right triangle that means these angles have to be 45 degrees and you can take the inverse tangent of Θ, the inverse tangent of this vertical divided by this horizontal if you wanted and you would find that it's 45 degrees. Okay! So the net electric field is going to be E prime that we just found plus E d, which is on the diagonal away from the center minus E m, which is on the diagonal towards the center and we are defining positive and minus the way we like... we can say this is the positive direction and we are gonna say that this is the negative direction. So E d which is... d is the charge on the far diagonal of the square is kq... I said b there because I am trying to write everything in terms of the same factors so E b, E c or q b, q c and q d are all interchangeable so instead of writing q d, I'm writing q b since b is what I used here and what I used here already. Okay! So kq b over r d squared and r d squared is the side length of a square squared plus the side of the other square squared so 2 times l squared. In other words, r d is square root 2 times the side length of the square. So the length of this hypotenuse of this entire square is root 2 times one of the side lengths. So we substitute that in for r d and so E d then is kq b over 2l squared. The next thing we want to know is what is the electric field due to the middle charge so that will be k times q m and I can't use q b here because the middle charge has a different magnitude than the corner charges so that's negative 1.00 nanocoulombs here. So we have to use q m divided by r m squared and r m squared is half this side length and half this side length so r m squared is one leg squared plus the other leg squared and that's what we are writing here. So r m squared then is 2 times l over 2 squared which is l squared over 2 because this is l squared over 4 times 2 makes l squared over 2. So l squared over 2 gets substituted in place of r m squared... this works out to 2kq m over l squared. There! Now we have expressions for each of these fields in terms of q b, q m and l all of which we know. So we have root 2 times kq b over l squared— that's what E prime is— and then plus kq b over 2l squared— that's what E d is— and then minus kq m over l squared— that's what E m is— and I am referring to each of these things here. And then we can factor out the k over l squared and multiply by root 2 times q b plus q b over 2 minus 2 times q m. So we plug in numbers: Coulomb's constant divided by the side length— 20.0 centimeters—and square that and we write 'centa' as times 10 to the minus 2 meters and then times square root 2 times 2.00 nanocoulombs plus 2.00 nanocoulombs divided by 2 minus 2 times 1.00 nanocoulomb and we get 411 newtons per coulomb and that's at an angle of 45 degrees above the x-axis to the left.
