Question
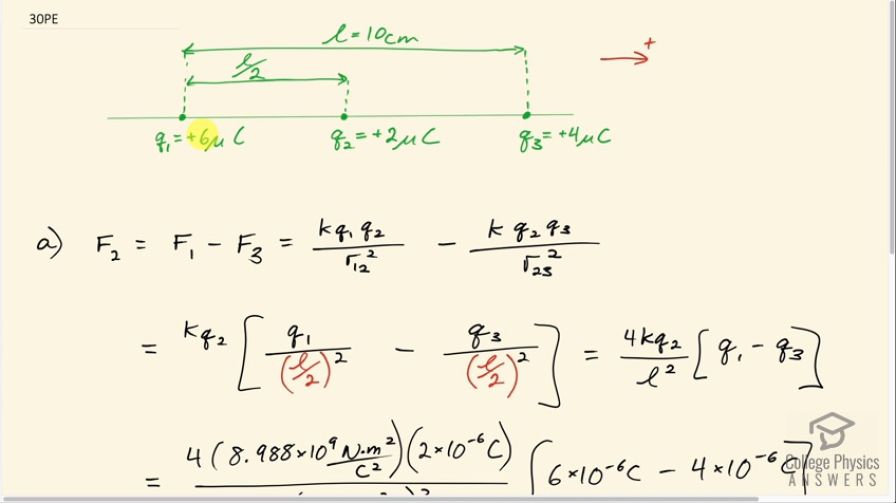
A test charge of is placed halfway between a charge of and another of separated by 10 cm. (a) What is the magnitude of the force on the test charge? (b) What is the direction of this force (away from or toward the charge)?
Final Answer
- The force is directed away from the charge.
Solution video
OpenStax College Physics for AP® Courses, Chapter 18, Problem 30 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. A 2 microcoulomb test charge is placed halfway between charge q 1, which is positive 6 microcoulombs and q 3, which is positive 4 microcoulombs; q 1 and q 3 are separated by 10 centimeters and so the distance between q 1 and q 2 is half of that... half of l which would be 5 centimeters. So the force on charge number 2 is gonna be force 1 minus force 3 and we get the sign by first establishing a coordinate system which is to say to the right is positive and then the charges that were put in here will all be positive and our negative sign just indicates direction. So the force due to charge 3 is to the left because it's going to repel charge 2 and so that makes the force due to charge 3 in the negative direction and so that's why there's a minus here and the force due to charge 1 will be a little bit bigger since it has a larger charge—6 versus 4 microcoulombs— and it is to the right and so it is positive. Okay! So the magnitude of the force due to charge 1 is Coulomb's constant times charge 1 times charge 2 divided by the distance between charges 1 and 2 squared and then we subtract from that the magnitude of the force due to charge 3 which is kq 2q 3 over the distance between charges 2 and 3 squared. The k and the q 2 can be factored out and we are left with kq 2 times q 1 over r 12 squared but r 12 is this distance here which is l over 2 so we can substitute l over 2 in place of r 12 and the distance r 23 is also half of l this is also l over 2 and so we substitute that in place of r 23. And then dividing by l over 2 squared is the same as multiplying by 4 over l squared so we have 4kq 2 over l squared times q 1 minus q 3. Then we plug in numbers and we have 4 times Coulomb's constant times 2 microcoulombs divided by 10 centimeters squared and writing in the substitution so the prefix is, you know, times 10 to the minus 6 for the prefix 'micro' and times 10 to the minus 2 for the prefix 'centa' and then multiply that by 6 times 10 to the minus 6 coulombs minus 4 microcoulombs, this works out to 14.38 newtons but since our charges are given with only one significant figure, we are going to have only one significant figure in our answer so this rounds to 10 newtons. And the direction of the force is away from the 6 microcoulomb charge and we know that because our answer is positive and we have defined positive to be to the right which is away from the 6 microcoulomb charge and we expected that right from the beginning anyhow because the distance between charges 1 and 2 and 2 and 3 are the same but charge 1 has a greater magnitude so we expect it to win this sort of contest and have a net force to the right.
