Question
(a) Find the electric field at the center of the triangular configuration of charges in Figure 18.53, given that , , and . (b) Is there any combination of charges, other than , that will produce a zero strength electric field at the center of the triangular configuration? The equilateral triangle has a side length of .
Final Answer
- No, the only configuration is
Solution video
OpenStax College Physics for AP® Courses, Chapter 18, Problem 23 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
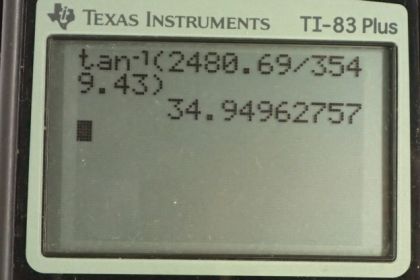
Calculator Screenshots
Video Transcript
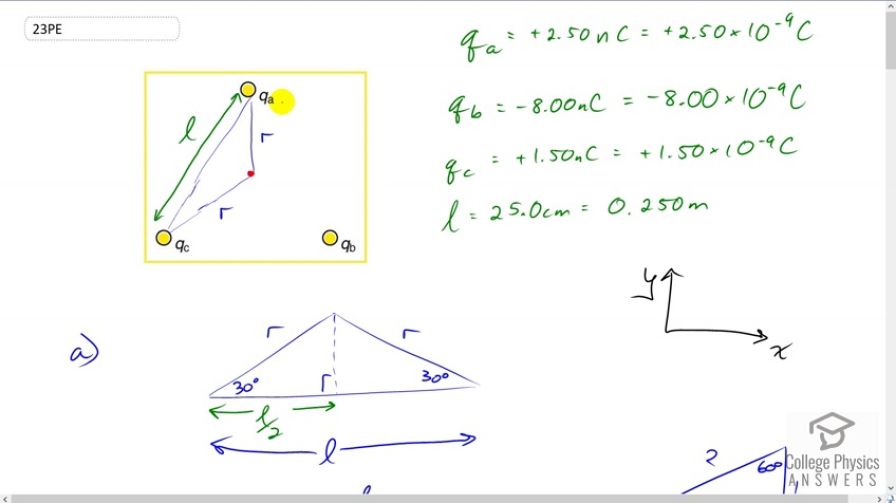
This is College Physics Answers with Shaun Dychko. We're going to find the electric field at the middle of this equilateral triangle, so at this point here. We're told that charge a is positive two and a half nano Coulombs, charge b is negative eight nano Coulombs, and charge c is positive one and half nano Coulombs. And the length of the side on this triangle is 25 centimeters. And I've converted each of these things into their base units, of Coulombs and meters. So, the first step is to figure out what is the distance r, which will be the same for each of these charges since the triangle is equilateral. Now, I've redrawn this triangle here, here and that's an isosceles triangle with two sides that are length r and then the base is length l. And if we cut in half, the altitude of an isosceles triangle intersects the base at a right angle and bisects the base. And so this side length here for this triangle, this is going to be l over two. And we're going to figure out r. So, we know that cosine of 30 degrees, and we know that this is 30 degrees by the way because a line going from the corner to the center of an equilateral triangle bisects the angle. And at the corner of the triangle, and we know that the angle of an equilateral triangle that's always 60 degrees because each angle has to be the same and they have to add up to a 180 as angles always do, triangles. And so being the same, each of them is going to be a 180 divided by three, so 60 degrees. And this line here is going to bisect the 60 to turn into 30 degrees. So that where 30 degrees comes from here in this picture. So cosine of 30 is going to be the adjacent over the hypotenuse. So that's l over two divided by r and we want to solve for r by multiplying both sides by r over cos 30 and we have r isl over two over cos 30. Now cos 30, you could plug into your calculator or I'll prefer to use a special triangle, of leg's one and the hypotenuse is two and this side is root three, and this angle is 60 and this is 30. And that means that cosine of 30 is root three over two. So we substitute that in, multiply top and bottom by two and that makes l over root three. So r is the side length of the triangle divided by root three. Now with that out of the way, we can think about all the forces that are on or all the electric fields that are on the center. So we'll consider the x direction first and so the x component of the electric field due to charge a is zero because electric field due to charge a is straight down because a is positive charge and so its electric field will go away from it. And we have our coordinate system set up the traditional way such that x is positive to the right and y is positive upwards. And we'll think about the electric field due to charge b, being a negative charge, electric field will go towards charge b and so its x component will be in the positive direction and let's draw this little electric field triangle here. This is electric field due to charge b, here's the center of the triangle and here's the x component that we're going to find in a second. And this angle here is 30 degrees, because you can imagine that the qb is here and this line from the center towards the corner is going to bisect this angle of the triangle. And so that makes this 30 down here and these two lines being these two lines being parallel make these interior opposite angles, and so they're equal. And so that makes this 30. And so it's the cosine of 30 multiplied by this hypotenuse E subscript b, is going to give E subscript x. And that's what this cos 30 comes from here. And so the electric field to the charge b in the x direction is going to be a positive direction. And notice I'm always thinking just about the magnitude of the charge here, so even though qb is a negative eight nano Coulombs, I will not substitute negative eight for qb here. Instead when I use that information to figure out direction and put that direction explicitly in front of the term and then substitute only the magnitude of the charge. So this x component of the electric field due to charge b will be on the positive direction, it's going to be Coulombs Constant times qb over the distance r squared times cosine of 30, cosine of 30 is root three over two, as we know from our special triangle. And there we go. And then the x component of the field due to charge c is going to be in the positive direction, as well, because charge c is a positive charge. And so its field will be up into the right. And so its x component will be up to the right. And so we have positive kqc over r squared times cos 30. And there we go. So the x component of the resultant then is the sum of the x components of each of the charges. And so they all have factors kqb root three over two r squared in them. And so we factor that out. And Eax is zero of course. And so we end up with this factored out times qb plus qc. And then I substitute in l over root three in place of r, because we need to figure that out at the beginning and then multiply top and bottom by three, so that this cancels after it gets squared, that's going to be a three below the l there. And this works out to three root three k over two l squared times qb plus qc. So let's plug in numbers and figure out what that is. So we have three root three times Coulombs constant divided by two times 0.25 meters squared times eight times ten to the minus nine Coulombs for qb plus one and a half times ten to the minus nine Coulombs for qc. Notice just substituting magnitudes of the charges in here, not plugging in the negative there. It's intentional that I did not put a negative eight for qb. And that works out to 3549.43 newtons per Coulomb and because it's positive, it's to the right. Then, we consider the y direction and so the y component of the electric field due to charge a is entirely, well it is just the field because it's entirely straight down. And so, with the negative in front of it because it's straight down, so that's negative kqa over r squared. And for electric field due to charge b in the y direction, it's going to be, well this charge b has a field that is down into the right. And so its y component is going to be negative. And this angle here is 30 and the opposite leg will find by going sine of 30 multiplied by the hypotenuse. It's the y that we are finding now. And so this is the opposite leg of this right triangle. And we use sine 30 times the hypotenuse to find it. And so we have sine 30 times negative kqb over r squared. And sine 30 is a half, based on this special triangle. Sine 30 is one over two. And then the y component of the field due to charge c is going to be positive because c is a positive charge, and so its field is up into the right and so it's y component is upwards. And so we have positive kqc over r squared times a half because that's what sine 30 is. And so to find the resultant y component, we add the components of each of these charges together. And they all have a factor k over r squared, so we factor that out. And then it's negative qa from charge a. And then negative qb over two and then plus qc over two and substituting r as l over root three. We end up with three k over l squared times negative qa minus qb over two plus qc over two. And then we plug in numbers. And of course, plugging in magnitudes over for each of these charges and having the sign as shown in the equation. And all this works out to negative 2480.69 newtons per Coulombs. And because it's negative that means it is downwards. So the magnitude of the resultant will be the square root of the sum of the squares of the components of the resultant. So that's square root of 3549.43 newtons per Coulombs squared plus negative 2480.69 newtons per Coulombs squared, giving us a resultant magnitude of 4330.4 newtons per Coulomb. Now because the x component is positive, it is to the right. And the y component is negative, it is down. And so our resultant is in this direction, down into the right. And so when we find this angle theta, we're going to take the inverse tangent of the y component of the field, divided by the x component of the field. And our answer will be such and such degrees, below the positive x axis. And so doing that, inverse tangent of the y component of the x component and I'm not putting in a negative sign there because I already conceive what the direction is based on this picture. We get 34.95 degrees below the positive x axis. And so our final answer is 4.33 with three centimeter figures times ten to the three newtons per Coulomb, 35.0 degrees below the positive x axis. Then, part b if that wasn't enough there's a part b. So, we're asked to figure out what configurations of charges would result in zero electric field in the center. Now, is having them all equal, the only one that works? Well, let's assume that they're not all equal. We have to at least assume that qb and qc are equal such that their x components cancel. And so with their equal, then they're going to have, there's going to be this field, also let's say they're positive, as well, equal and positive. That means the field due to charge b will be up into the left and the field due to charge c will be up into the right, and if they're equal magnitude charges than these fields will have x components that are the same. And they will cancel. And so, in the x direction, we'll have no x component due to charge a because of that field is going to be straight down. And component b, x component due to charge b and the x component due to charge c or b equal and opposite. And therefore no x component at all. And then in the y direction, we know that the y component of the field due to charge b will be kq over r squared times sine 30. And then, sine 30 being one half so that's kq over two r squared. And the y component due to charge c will be the same. And so, in order to balance that, the y component due to charge a which is just the field due to charge a since it's entirely straight down, will have to be the opposite of the sum of the y components of the fields due to charge b and c. So that's negative of kq over two r squared plus kq over two r squared, which is negative kq over r squared. But since this is equal to that, it means that qa has to be equal q. So, therefore, we've just kind of shown that that's the only thing that works, qa has to be the same as qb which has to be the same as qc. And that's the only configuration that results in zero electric field, the center of an equilateral triangle.
Comments
How do you know that its 25cm
Thanks for the clarifcation for the last question. My 2nd question is how do you know which side to find. Why do we try to solve for qc, why not qb?