Question
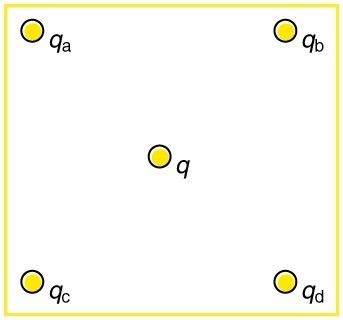
(a) Using the symmetry of the arrangement, determine the direction of the electric field at the center of the square in Figure 18.52, given that and . (b) Calculate the magnitude of the electric field at the location of , given that the square is 5.00 cm on a side.
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 18, Problem 19 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. In part a of this question, we’re going to figure out what is the direction of the electric field in the center of this square. We’re given the charges a and b are both negative one microcoulomb and charges c and d are both positive one microcoulomb, which means the electric field due to all of these charges are going to be in the upward direction at the center, but not precisely upwards although it works out to that in the end. Here’s the electric field due to charge a, here’s the electric field due to charge b, and here’s the electric field due to charge d, and then here’s the electric field due to charge c. They are all of equal magnitude, and these two are collinear, they are along the same line here, they are both at 45 degrees pointing to this corner, and these are both pointing to that corner. And the x components of all of these four vectors are going to cancel, because there are two to the right and two to the left of equal magnitude and so there is no x component at all. And so the y component of each of these four vectors will add together and they are all of the same magnitude and it’s going to end up with an electric field straight up. So that’s the answer to part a. Now in part b, we’re going to figure out what is the value of that electric field, the magnitude of it. First we need to know what is the distance between the charge in the center, and so here I’ve drawn a special triangle because we have a 45 degrees right triangle here, and the sides are length one, one and root two. This is a nice special triangle to remember, the other one by the way is one, two, root three, where you have 60 degrees and 30 degrees. The special triangles always come in handy. So what this means is that if we have a right triangle in our actual question with legs of length l over two, and so we’re going to be multiplying each leg here by l over two, which is five centimeters over two. In which case the hypotenuse is going to be five over two multiplied by root two, which works out to five over root two. That’s the way I think about it, but maybe you have a preference for different method, which would be to say well, I know that sine of 45 degrees is the opposite which is l over two, divided by the hypotenuse which is r. This five over two is l over two. And I want to solve for r, in which case r is going to be l over two divided by sin 45, but sin 45 is one over root two, or you can get its decimal form, plug that in into your calculator. Either way, you’ll get the same answer. So it’s l over two times one over, or divided by one over root two, so multiply top and bottom by root two, and these cancel, leaving us with l root two over two, which is l over root two. That’s what we have here, l being five. Now the electric field is going to be four times one of them, multiplied by sin 45. Sin 45 getting the y component of one of them, sin 45 is one over root two, and E, electric field due to one of the charges is kq over the distance r squared, and then r is five over root two centimeters, and then we convert that into meters by multiplying by one meter for every 100 centimeters. We square that denominator and then we have four times Coulomb’s constant times one microcoulomb, and then multiply that by one over root two to get the y component, and we get 2.03 times ten to the seven newtons per coulomb upwards.
