Question
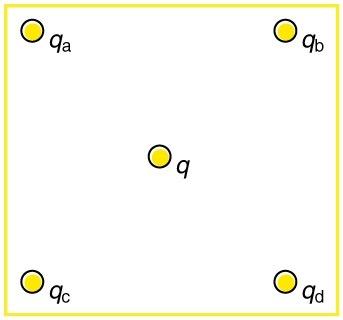
Using the symmetry of the arrangement, determine the direction of the force on q in the figure below, given that and . (b) Calculate the magnitude of the force on the charge , given that the square is 10.0 cm on a side and .
Final Answer
- Straight down
Solution video
OpenStax College Physics for AP® Courses, Chapter 18, Problem 18 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. In part (a) of this question, we are supposed to use the symmetry of this configuration of charges to figure out what the net force direction would be on this charge in the middle of a square. So charges a and b both have positive 7.50 microcoulombs on them and charges c and d are both negative 7.50 microcoulombs. So if we consider just charges a and b at the top here, charge a will exert a force this way on this center point and charge b will exert an equal magnitude force this way on the center point and these arrows are both going to be 45.0 degrees below horizontal but they are gonna be in opposite directions horizontally speaking and those horizontal components of these two forces will cancel and we'll be left with only their vertical components adding up. So this will be the vertical component of one of them added to the vertical component of the other and together they will make a force that is straight down. Now this same picture applies to these bottom corners as well because these are negative charges and so they are going to pull a positive charge in the middle towards them and the same analysis will apply and the horizontal components will cancel leaving us with just the vertical component downwards and so this could be the vertical component from charge a and this could be the vertical component from charge b and this could be again vertical component from charge d and then c and you get the idea... all these vertical components add together so that the total net force on this charge in the middle will be four times the vertical component of one of the force due to one of the charges. Okay! So the answer to part (a) is straight down based on the symmetry here and the horizontal components on either side canceling. Alright! And then in part (b), we are meant to figure out what is the magnitude of the force on this charge in the center so we have to do some calculations given the side length of a square of 10.0 centimeters and this charge in the middle is 2.00 microcoulombs. So the net force will be four times the vertical component of one of the force due to one of the charges and it's gonna be straight down and so the vertical component of one is going to be Coulomb's constant times the charge in the corner—q a— times the charge in the center—q— divided by the distance from a corner to the center, which is r squared and then find its component that is vertical and we'll multiply by sin 45 to get that... or cos 45, whichever way you wanna look at it. I guess if I put this 45.0 degree angle down here then it will make more sense to say sin 45 because sin 45 is this opposite divided by this hypotenuse and we'll multiply the hypotenuse by this sin 45 to get this vertical component to the force. Okay! So r squared—this is the hypotenuse of this right triangle here— its length squared is gonna be the length of one leg which is half the side length of the square l over 2 squared plus again half the side length of the square to get to the middle horizontally and then we square that and so that's 2 times l over 2 all squared which is l squared over 2... I mean it's l squared over 4 but then multiplied by 2 makes l squared over 2. So that is r squared and that can be substituted into the denominator here, which normally I do in red so let's click that. And then we have 2 times kq aq over l squared times sin 45 is the vertical component of one of the forces and all the forces are the same magnitude because they all have the same magnitude charge and they all have signs such that they all point down. Okay! So we can plug this in for F y and so we have F net then is 4 times all of this which is 8 times kq aq times sin 45 over l squared and now we can plug in numbers. So we have 8 times Coulomb's constant times 7.50 microcoulombs times 2.00 microcoulombs times sin 45 divided by 10.0 centimeters squared and writing all these things in base units with times 10 to the minus 6 instead of 'micro' and times 10 to the minus 2 instead of the prefix 'centa,' we end up with 76.3 newtons is the net force and that is downwards.
