Question
(a) Two 0.500 g raindrops in a thunderhead are 1.00 cm apart when they each acquire 1.00 mC charges. Find their acceleration. (b) What is unreasonable about this result? (c) Which premise or assumption is responsible?
Final Answer
- This acceleration is too large, and would break apart the rain drop.
- is unreasonably large. A charge would be more reasonable. See the video for an explanation as to why.
Solution video
OpenStax College Physics for AP® Courses, Chapter 18, Problem 65 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
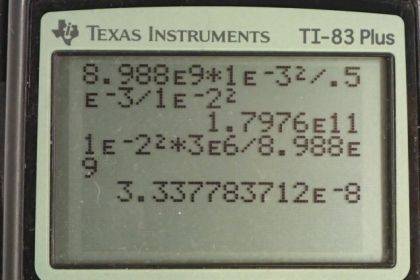
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. We have two raindrops with a mass of 0.5 grams and we convert that into kilograms, and they each have a charge of one millicoulomb, which is one times ten to the minus three coulombs, and they are separated by one centimeter which is one times ten to the minus two meters. And so here’s a drawing of the two drops, each with a mass of m and charge q. And we’re going to find the drops’ acceleration. And so the force equals mass times acceleration, and that’s going to be the electrostatic repulsion, which is Coulomb’s constant times the one charge times the next charge, divided by the distance between them squared. And this q times q can be written as q squared. And we’ll solve for acceleration by dividing both sides by m, and we get a is kq squared over mr squared. So this is Coulomb’s constant times the charge squared, divided by the mass and multiplied by the separation between them squared, this gives 1.80 times ten to the 11 meters per second squared. This result is much too large and it would break apart the raindrop. The reason that we’re getting such an unreasonable result is that the charge on each drop is unreasonable. It’s quite possible for drops to be separated by one centimeter, that’s fine, but it’s this charge of one millicoulomb. Even though there’s a prefix in milli, which normally means that you’re talking about something small, when you’re talking about coulombs, one millicoulomb is actually a very large amount of charge. And we can get a sense for what charge is reasonable by looking at problem 59 where they say the electric field that causes the air to start conducting electricity, which is caused by the air having what’s known as dielectric breakdown in which case particles in the air become ionized and they become conductors. In other words, it’s the electric field that would cause a spark. Sparks happen when electric fields exceed this number which we’re told in problem 59 and they occur because the air particles are broken apart into charge components. And that’s called dielectric breakdown. So let’s find out what amount of charge would result in this electric field at distance one centimeter away. Electric field from a point charge is Coulomb’s constant times the charge divided by the distance from the charge squared, and we’ll solve this for q by multiplying both sides by r squared over k and then switching the sides around. So the charge is r squared times electric field divided by Coulomb’s constant, so that’s one centimeter squared times three times ten to the six newtons per coulomb, maximum electric field before sparks happen, divided by Coulomb’s constant, which is 3.34 times ten to the minus eight coulombs. Now this is an amount of charge that would be reasonable on the drops, which is way way way less than the one millicoulombs given to us in the problem.