Question
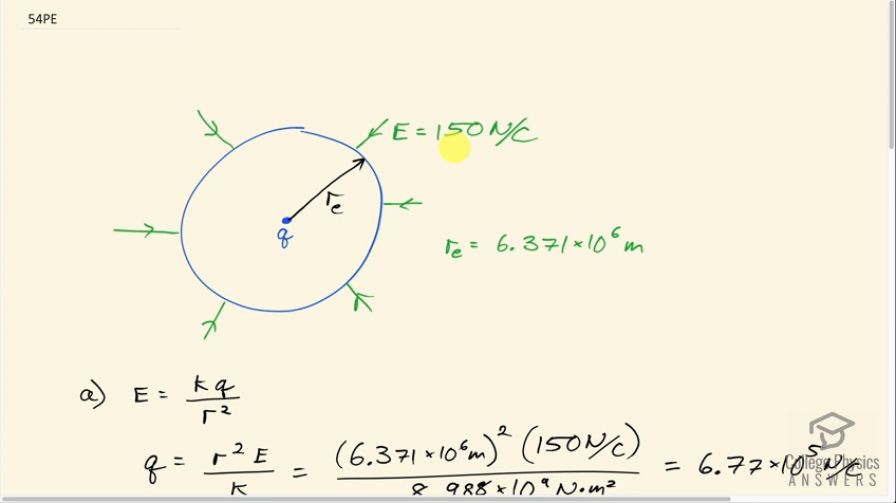
Earth has a net charge that produces an electric field of approximately 150 N/C downward at its surface. (a) What is the magnitude and sign of the excess charge, noting the electric field of a conducting sphere is equivalent to a point charge at its center? (b) What acceleration will the field produce on a free electron near Earth's surface? (c) What mass object with a single extra electron will have its weight supported by this field?
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 18, Problem 54 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. The Earth has an electric field pointing towards the center of magnitude 150 newtons per coulomb; because it's pointing towards the center that means that this charge that we imagine to be here is a negative charge in order to have field lines pointing towards it. So the electric field is a distance 6.371 times 10 to the 6 meters on the surface away from the center and we are gonna figure out what charge we imagine is at the center. So we have the electric field is Coulomb's constant times the charge divided by the distance from it squared and we can solve this for q by multiplying both sides by r squared over k. So q is r squared times electric field strength divided by Coulomb's constant. So that's 6.371 times 10 to the 6 meters squared times 150 newtons per coulomb divided by Coulomb's constant and that is negative 6.77 times 10 to the 5 coulombs. Now this arithmetic here worked out to a positive number but we know from the physics here that this charge must be negative and so we can put the negative sign there. In part (b), we are asked what acceleration this field would produce on a free electron? So if the electric field is the only force on the electron then it would be the net force in which case this force would be mass times acceleration and the force is given by the electrostatic force and so it's the charge multiplied by the field. And so these are equal and we can solve for a by dividing both sides by m. So the acceleration is q times electric field divided by mass. So this is the elementary charge on an electron multiplied by the electric field strength on the surface of the Earth divided by the mass of an electron that I looked up with a search engine this works out to 2.63 times 10 to the 13 meters per second squared and this direction would be upwards because these field lines point in the direction of force on a positive test charge and so given that we are working with a negative electron here, the force on it will be in the opposite direction to the electric field lines and so it will be away from the center of the Earth or away from the surface. Okay! In part (c), what mass object with a single electron will have its weight supported by this field? And so the weight is downwards it's going to be equal to mass times gravitational field strength and the electrostatic force will be upwards equal to this single electron charge multiplied by the electric field on the surface of the Earth. So these forces are equal and so we have mg equal to q times E and we can divide both sides by g to solve for m. So m will be the elementary charge multiplied by the electric field strength on the surface of the Earth divided by gravitational field strength, this works out to 2.45 times 10 to the minus 18 kilograms.

