Question
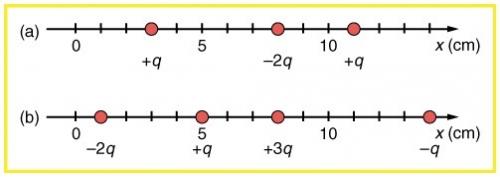
(a) Find the total electric field at in Figure 18.51(b) given that . (b) Find the total electric field at in Figure 18.51(b). (c) If the charges are allowed to move and eventually be brought to rest by friction, what will the final charge configuration be? (That is, will there be a single charge, double charge, etc., and what will its value(s) be?)
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 18, Problem 15 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. So we’re looking at the charge distribution in part b here, and part a of the question asks us what is the electric field at x equals one centimeter. So I wrote the subscript 1 there for the electric field at one centimeter and there is a charge there at the first tick. And so because there is a charge there, the electric field due to this particular charge will be k times negative 2q divided by zero, because there is no distance between this charge and the position of interest, because it’s there at the same place. And dividing by zero, well mathematically this means it’s undefined but in the physical context, we would say that well it’s not truly zero, it’s probably something really really really close to zero. For truly zero, there is no answer to what the electric field would be. But really really close to zero, it approaches negative infinity because the charge is negative. So the electric field approaches negative infinity at x equals one centimeter. And now in part b, we’re asked to find the electric field at x equals 11 centimeter, so at this tick mark here. So we’re going to have an electric field due to the charge at position one, we’ll have an electric field due to the charge at position five, and due to charge at position eight, and due to charge at position 14. Now each of these expressions are gonna have a factor k, the Coulomb’s constant in front of it so I just factor it out. And we’re gonna have, for the, so first of all let’s figure out the coordinate system, to the right is positive, so any field that points to the left we’ll say it’s negative, and any field that points to the right will be positive. And the place for that will get a bit confusing is when we deal with this particular charge, the electric field due to the charge at position 14. It’s going to be a positive because what I’m doing here is I’m writing down what is the sign of the electric field. And so because this is a negative charge, it’s going to be creating a field line that is pointing this way, towards it, and so at position 11, the field line will be going to the right due to this charge. And so that’s why we’re going to put a positive here, because it’s directed to the right. So never mind the fact that the q is negative but we’ve dealt with all that, we just want to put in what is the sign here according to direction. So it’s to the right, and so we have positive. There. Now. The electric field here due to the charge at position one will be to the left, towards this charge, and so it’s negative 2q over r1 squared, r1 being the distance between the position of interest at x equals 11 and x equals one. And then add to that the charge due to or the electric field due to this charge, and that is going to produce field lines that are to the right, so that’s going to be q divided by r5 squared plus 3q over r8 squared and then plus q over r14 squared that we’ve already talked about. And then plug in some numbers. We’re told that the charge q is five nanocoulombs and nano is the prefix times ten to the minus nine, and so we have, we also can factor out the q by the way, so we did that here. So we have kq times negative two over r1 squared plus one over r5 squared plus three over r8 squared plus one over r14 squared. And then substitute in numbers. So we have Coulomb’s constant times the charge and then times negative two over 11 centimeters minus one centimeter squared, and then plus one over 11 minus five, so this is the distance between the position of interest and the location of the charge, and then we have plus three over 11 minus eight and then plus one over 14 minus 11, so there’s three units distance between this charge and position of interest. Now I’ve used centimeters there which we have to accommodate for because we can’t have centimeters mixing with the meters here, and so we’ll have to convert. And so I didn’t have room to write this multiply so I wrote it down here. So we’re multiplying by 100 centimeters for every meter and we’re doing that twice, and so that’s converting the differences which are in centimeters squared in the denominator into meters squared in the denominator. This works out to 2.03 times ten to the five newtons per coulomb, and that is positive and so it’s to the right. Now in part c, we’re asked to say what is the final charge going to be if these are all left to move around by themselves. And well these two are going to repel each other, because these two are both positive. And they will repel each other and also at the same time attract this one here, and so this charge and this one are going to collide and turn into a single charge of positive 2q at the end, so that accounts for these two. And that will happen somewhere between them, hard to say where exactly, depends on how much friction there is I guess. And then these two will combine, somewhere over here and result in a charge of negative q, and so these are gone, let’s make that red, there. And now you have a negative q and a positive 2q, and those will attract and combine somewhere between them to result in a charge of positive q in the end. So there we go. Positive q will be the final charge.
