Question
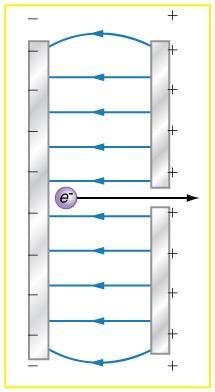
A simple and common technique for accelerating electrons is shown in Figure 18.55, where there is a uniform electric field between two plates. Electrons are released, usually from a hot filament, near the negative plate, and there is a small hole in the positive plate that allows the electrons to continue moving. (a) Calculate the acceleration of the electron if the field strength is . (b) Explain why the electron will not be pulled back to the positive plate once it moves through the hole.
Final Answer
- The net electric field outside of the plates is zero. See the solution video for an explanation as to why.
Solution video
OpenStax College Physics for AP® Courses, Chapter 18, Problem 53 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. We have two charged plates, charged with equal magnitude but opposite signs. This plate is positively charged and this one is negatively charged and they create an electric field between them of 2.5 times ten to the four newtons per Coulomb. There is an electron introduced here probably from some hot filament that is just emitting electrons because it's hot. And this electron will be repelled from the negative plate and attracted to the positive plate or you could think of it as it's going to be moved by this electric field, in other words. And it's going to zip out through this hole, in the positive plate. And when it gets beyond this positive plate, there is no electric field here at all. And I guess that's part b and we'll talk about that in a second. But first of all, we'll talk about why, in a second. For part a, we're asked to figure out what is the acceleration of this electron. We'll it's charge as the elementary charge and here's the mass of an electron. And we know that the net force on electron is mass times acceleration and we'll divide both sides by m to solve for a. So a is force which is electric field strength times the charge divided by m. So that's two and a half times ten to the four newtons per Coulomb times 1.60 times ten to the minus 19 Coulombs divided by 9.11 times ten to the minus 31 kilograms. And this gives 4.39 times ten to the 15 meters per second squared. So, the electron is not attracted to this positive plate when it is beyond that plate because there's no electric fields here and the reason for that is that the electric field due to the positive plate which is directed like this, away from the plate. I'm drawing the electric field due to the positive plate on the right hand side of the positive plate. That electric field is of equal magnitude to the electric field resulting from the negative plate which is directed towards the negative plate. So, you see the blue field due to the positive plate and the green field to the negative plate are on opposite directions and they're equal magnitudes. And that might be a surprise because you might think, well since we're closer to the positive plate, shouldn't the field due to the positive plate be greater and the answer is no. This whole kq over r squared business that we're used to for electric fields, does not apply. This is for a point charge. Now for a large plate, these field lines are parallel and that's intentional to draw it in parallel here and it means that the electric field does not change with distance. So when you go farther and farther away from the plate, the field's magnitude does not change. And this is true with the assumption that the plate is very large. And so at this point, the electric field due to the positive plate is the same as electric field due to the negative plate, just on opposite directions. And so this is why they make and debt electric field to zero on the right hand side of the positive plate.
