Question
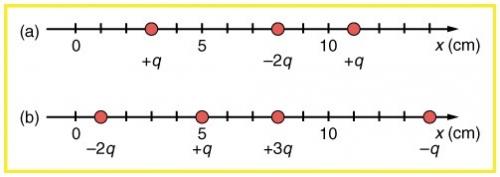
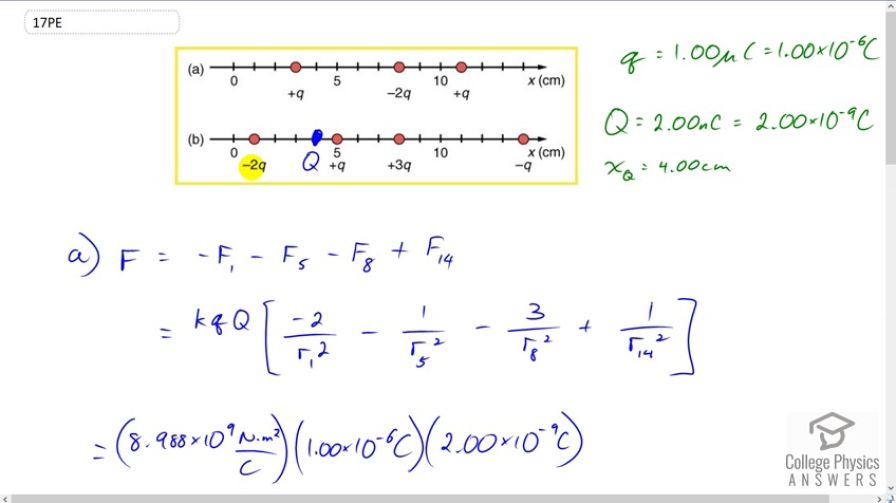
(a) Find the total Coulomb force on a charge of 2.00 nC located at in Figure 18.51 (b), given that . (b) Find the x-position at which the electric field is zero in Figure 18.51 (b).
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 18, Problem 17 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
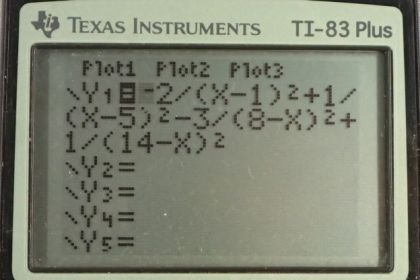
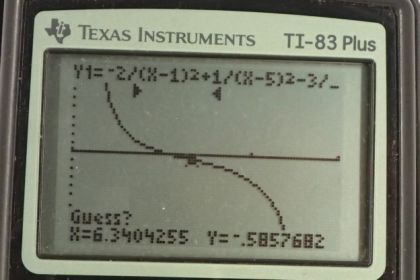
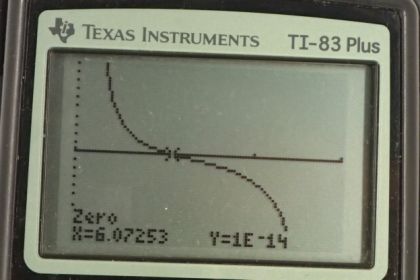
This is College Physics Answers with Shaun Dychko. We’re looking at part b of this picture, so it’s this charge distribution in this bottom row here. And little q we’re told is one microcoulomb, so that’s one times ten to the minus six coulomb. And we’re asked to find out what is the force on this charge, called capital Q, located at x equals four centimeters, with a charge of two nanocoulombs which is two times ten to the minus nine coulombs. So the force is going to consist of the net force, it’s going to consist of four forces on this charge, one due to each of these other charges that are along the line. And there’s going to be a force due to the charge at position one, and I put a minus in front of it to indicate its direction because it will attract this charge capital Q to the left, and so we’re going to define our coordinate system as positive to the right. And so that means the force due to the charge at position one is negative. And the charge at position five will be repelling this capital Q, and so it also will be exerting a force to the left, and so we have a minus force due to charge at position five. And then at position eight likewise, because these charges are the same, they repel and so that’s going to exert a force to the left. And then the charge at position 14 is negative, and it’s attracting the capital Q charge and it will exert a force to the right, and so we have a positive force due to charge at position 14. So then we use Coulomb’s equation to write this next line, what would the magnitude of the forces be. And each of these expressions are gonna have a k, little q, capital Q in them, and so I factored that out, and so we just have negative two over r1 squared, r1 being the distance between the charge at position one and this charge capital Q at position four. And the negative two comes from the fact that, well the negative comes from the fact that the force is to the left, it’s not because the charge is negative 2q. I mean this charge over here is negative q but I have a positive in front of that one because it is directed to the right. And then we have a minus one over the distance between the charge at position five and capital Q squared, and then minus three over the charge at position eight, its distance from the charge at position four squared, plus one over r14 squared. So then we plug in a whole bunch of numbers. So we have Coulomb’s constant of 8.988 times ten to the nine Newton meters squared per coulomb, times one times ten to the minus six coulombs is the magnitude of charge little q, and capital Q has a charge of two times ten to the minus nine coulombs. Then we multiply that by all these expressions in the bracket. So each of these terms are negative two over four centimeters minus one squared, minus one over five centimeters minus four centimeters squared, minus three over eight centimeters minus four centimeters squared, plus one over 14 minus four centimeters squared. And since we’re using centimeters in the denominator here, we need to convert those into meters, so we multiply by 100 centimeters per meter and we do that multiplication twice. And we end up with negative 0.252 newtons, and so because it’s negative, it’s to the left. So the force is 0.252 newtons to the left. Now for part b, we’re asked to find out where is this electric field going to be zero. Now we can narrow things down a bit just without any equations. We can think about any position to the right of this charge, it’s impossible for the field to be zero anywhere there, because if you’re at a position here, looking back you’ll see a negative q and then a positive 3q and a positive q and a negative 2q, all this works out to, well this is four to the plus and then three minus, so if you go far enough away, this looks like a plus q single point charge. And so there’s always going to be a field pointing to the left, sorry to the right, anywhere here. And for the same reason, there’s always going to be a field pointing to the left anywhere here. This is because there’s going to be a net charge on one side of you but nothing on the other side, so there’s no way for this picture to change when you’re beyond the extreme extremities here. Then, we’ll think about the position between here and here. When looking to the, if you’re here say, if you look to the right, you’ll see a total charge of plus four minus one which is plus three, and you look to the left and you have a charge of negative 2q. But the thing is, they both point to the left. The negative 2q charge will be attracting a point charge here to the left, and this positive 3q on the right hand side will be repelling also to the left, and so it’s not possible for there to be a zero electric field in this interval either. And likewise here, we’re going to have a total of positive three to the left of this position, and negative one q to the right, and so for the same reason, we’re going to have electric field always to the right anywhere in this interval. So that means, we’ve narrow things down to just in here. So in here, it is possible for electric field to be zero. And we’re going to create an expression, and then we’re going to solve it graphically using a graphic calculator and I’m going to include a bunch of screenshots below this video to explain what buttons to press to graphically solve this equation. So but just to make sure you know where each of these terms come from, the electric field is going over be k times little q, which I’ve factored out from each term, times negative two over whatever the position ends up being, we’ll call it x, minus the position of this particular charge which is one centimeter, and we square that, plus one over the unknown position x minus five centimeters and we square that, minus three over eight centimeters minus x. You could have gone x minus eight centimeters I guess, doesn’t make any difference because when you square it, you end up having a positive anyway, but I like to think of it this way. And then plus one over 14 minus x squared, and these numerators are the coefficient, so each of these charges by the way, not strictly that way though because this one is a positive one, so the sign that I’m including amongst these terms is according to the direction of the field due to that charge, but the magnitude of this numerator is the magnitude of the coefficient of each of these charges, that would be a more precise way of saying it. Now divide both sides by kq, because this whole electric field has to equal zero we’re told, and so we get this. Now this is something you can plug into your calculator, solve graphically and determine that x equals 6.07 centimeters. When there is a, at this position here 6.07 centimeters right here, that’s where electric field is zero.