Question
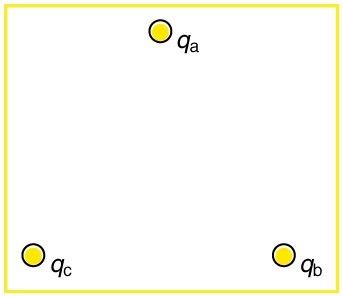
(a) Find the electric field at the location of in Figure 18.53, given that and . (b) What is the force on , given that ?
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 18, Problem 22 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. We are given charges on corners of an equilateral triangle: charge q c is negative 5.00 microcoulombs and charge q b is positive 10.0 microcoulombs and this point up here is... there's no charge there for part (a) of this question, we assume that it is just a point in space that we want to find the electric field at and all these points are on an equilateral triangle which is to say that the side lengths are the same— 25.0 centimeters— and that also means that the angles inside the triangle are all 60 degrees as they are for every equilateral triangle. So we have to find the electric field at this position given these two charges here. So this is the position of interest and it's going to be a field directed away from charge b there and this will be at an angle of 60 degrees with respect to horizontal because you can imagine this line here and this line along this side here being parallel and this is the transverse between those parallel lines and this angle here is what's drawn here and it's a corresponding angle to this one which is 60 degrees and corresponding angles are equal. Okay! And we also have a field pointing towards charge c because since it's negative, it's going to attract a positive test charge that could hypothetically be put here and it will therefore create a field in this direction— and that's what I have drawn here in blue— and this is the field due to charge c and it's going to be at an angle of 60 degrees below horizontal because this is an interior opposite angle to this one. Now the resultant is gonna be the sum of these two vectors and we'll have to figure out the components of each of these vectors and then add the x-components together and add the y-components together and then use Pythagoras to figure out the magnitude of the resultant and then use inverse tangent to figure out the direction. Okay but one step at a time! First let's establish our coordinate system: we'll suppose that to the right is positive and up is positive as usual convention and then in our further work to do with positives and negatives, the only positive and negative we are going to be concerned with is the one that indicates direction so the fact that this is a negative charge is already accounted for in saying that this y-component is negative because it's downwards in other words. This x-component due to charge b is negative because it's in the negative direction to the left despite the fact that this charge q b is positive so the sign is going to indicate direction... ignore the positives and negatives that's already accounted for in the fact that we have made these vectors in these directions as drawn. I drew this special triangle here so that we... I don't know... it just makes it a bit cleaner when we are doing cosine of 60 degrees, we can write it as 1 over 2 and sin 60 is root 3 over 2 opposite over hypotenuse for sin and then adjacent over hypotenuse for cos. So the x-component of the electric field at position a— this is the x-component of the resultant of electric field b and c in other words— is going to be negative E b x and then minus E c x so these minus signs are therefore indicating direction and then everything else that I plug in is going to be just magnitudes in this term here for E b and E c. So the x-component of the field due to charge b will be cos 60 multiplied by the field strength due to charge b because this is the adjacent leg of this triangle in black and to find the adjacent leg, we multiply E—the hypotenuse—by the cos of this angle which is 60 and then minus from that E c times cos 60. Now E b is the Coulomb's constant times the charge b divided by the length from point b to point a squared and that's the side length of a triangle which is l so it's kq b over l squared and the field strength due to charge c is the Coulomb's constant times charge c divided by its distance which is also l squared so then we plug those things in for E b and E c. So E a x then is negative kq b over l squared times cos 60 minus kq c over l squared times cos 60 and we can factor out this negative kcos 60 over l squared from both these terms and multiply it by q b plus q c and then this cos 60, I replaced with one-half. So that's negative Coulomb's constant divided by 2 times 25.0 centimeters written as 25.0 times 10 to the minus 2 meters— that's the side length of a triangle here— and square that, multiply it by 10.0 microcoulombs plus 5.00 microcoulombs and that makes negative 1078560 newtons per coulomb. Okay! And then we have to consider the y-component of this resultant electric field at position a and it's going to be positive E b y because the y-component of the field due to charge b is in the upward direction and then minus the y-component of the field due to charge c and it's minus because that is in the downward direction which we have said is negative. So that's kq b over l squared— the magnitude of the field due to charge b—times sin of 60 because this is the opposite leg and we use sin 60 times the hypotenuse to get this opposite leg. And then minus kq c over l squared times sin 60 and then the k times sin 60 over l squared can be factored out and also replacing sin 60 with root 3 over 2 because it's a special triangle, we can give it sin an exact form—opposite over hypotenuse—root 3 over 2. And so we have Coulomb's constant times root 3 divided by 2 times 25.0 centimeters squared times 10.0 microcoulombs minus 5.00 microcoulombs and that works out to 622707 newtons per coulomb. So now we find the magnitude of the field which will be the square root of the x-component squared plus the y-component squared. So I have plugged in this x-component, squared it, plus this y-component, square that, take the square root of that sum and you get 1.25 times 10 to the 6 newtons per coulomb. And then to find the direction, let's just plot a picture here: we have this y-component that's positive so it's upwards and we have this x-component that's negative so it's to the left and so we have this angle Θ here that we want to find and it will be the inverse tangent of the opposite divided by the adjacent so it will be the inverse tangent of the y-component divided by the x-component and that is 30.0 degrees above the x-axis to the left. So the final answer for part (a) is that the field at position a is 1.25 times 10 to the 6 newtons per coulomb, 30.0 degrees above the x-axis to the left and you have to say to the left because otherwise this would also be 30.0 degrees above the x-axis but that's to the right so we have to distinguish between this direction versus this one by saying to the left. And if you wanted a totally unambiguous way of saying it without using the word 'to the left' then you would have to give your angle in standard position and that would be 180 minus 30 so that would be 150 degrees. Okay! Anyway... the force on a charge of positive 1.50 nanocoulombs at position a is a question for part (b). So the force would be the charge mutliplied by the field so that's 1.50 times 10 to the minus 9 coulombs times 1.2454 times 10 to the 6 newtons per coulomb and you get 1.87 times 10 to the minus 3 newtons, 30.0 degrees above the x-axis to the left.


