Question
A toboggan with two riders has a total mass of 85.0 kg. A third person is pushing the toboggan with a force of 42.5 N at the top of a hill with an angle of 15°. The force of friction on the toboggan is 31.0 N. Which statement describes an accurate free-body diagram to represent the situation?
-
An arrow of magnitude 10.5 N points down the slope of the hill.
-
An arrow of magnitude 833 N points straight down.
-
An arrow of magnitude 833 N points perpendicular to the slope of the hill.
-
An arrow of magnitude 73.5 N points down the slope of the hill.
Final Answer
(b)
Solution video
OpenStax College Physics for AP® Courses, Chapter 4, Problem 23 (Test Prep for AP® Courses)

vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
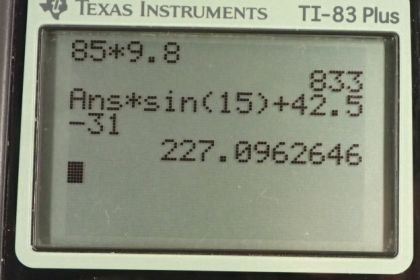
This is College Physics Answers with Shaun Dychko. The free body diagram of this toboggan consists of gravity straight down and there's a component of which is parallel to the slope. So this dotted line here represents the component of gravity that's down the slope. The hill has a 15 degree incline. There's force of friction directly up the slope of 31 newtons and there is a force applied by some third person down the slope of 42.5 newtons, and the mass is 85.0 kilograms. So, when we do the free body diagram we have to figure out which one of these four options is an accurate part of our diagram. Well, when we calculate gravity downwards it's 85 kilograms mass times gravitational field strength of 9.8 newtons per kilogram. That gives 833 newtons. So already we can see that part B is going to be our answer because there's an arrow of this magnitude pointing straight down. Now we could a bit further though just to see what happens, maybe there is two answers. So the parallel component of gravity is force of gravity times sine of theta because this angle here is equal to the angle of the slope. Then that plus the force of the person both downwards in the positive direction say, down the slope and then we'll take that to be positive, and then the force of friction is minus 'cause it's going up the slope. This is 833 newtons time sine 15 plus 42.5 minus 31 gives 227 newtons is the net force down the slope. That doesn't appear anywhere in our options so we're pretty safe with going with this option B, an arrow of magnitude 833 newtons points straight down.