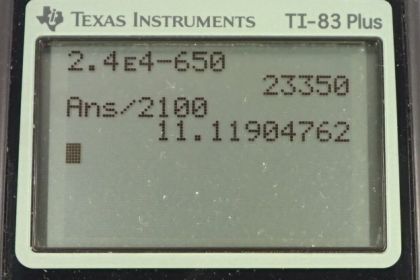
Question
(a) If the rocket sled shown in Figure 4.32 starts with only one rocket burning, what is the magnitude of its acceleration? Assume that the mass of the system is 2100 kg, the thrust T is , and the force of friction opposing the motion is known to be 650 N. (b) Why is the acceleration not one- fourth of what it is with all rockets burning?
Final Answer
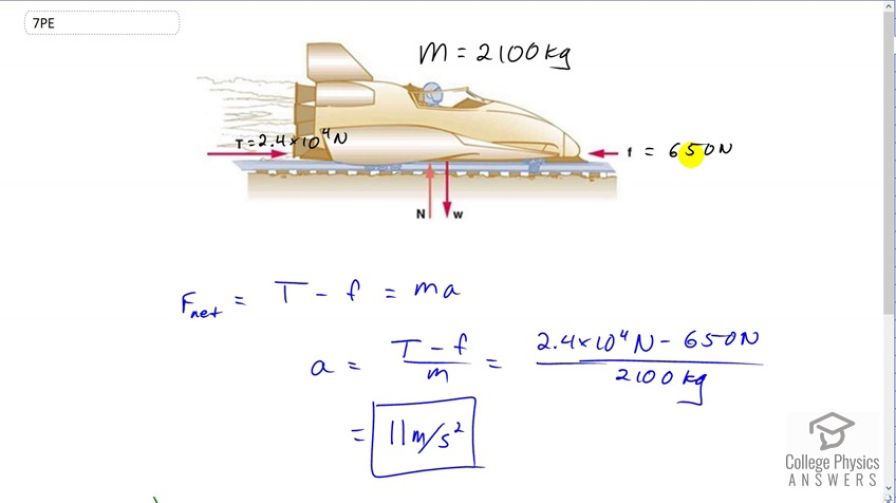
a)
b) since the friction force is still the same as in Example 4.2
Solution video
OpenStax College Physics for AP® Courses, Chapter 4, Problem 7 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. This rocket sled has a mass of 2100 kilograms. There is a friction force small f, of 650 newtons pointing to the left and one of the thrusters is going and it's producing a thrust of 2.4 times ten to the four newtons. In this question we're asked to find out what the acceleration of the rocket sled will be. So the net force is going to be all the forces to the right added together, minus all the forces to the left added together. There is only one to the right, that's the thrust, and there's only one to the left and that is friction. That will equal mass times acceleration as the net force always does. We'll solve for acceleration by dividing both sides by m and then switching the sides around, and we're thinking just about these parts here. You can ignore this part here. Then acceleration is the thrust minus friction divided by mass. So that's 2.4 times ten to the four newtons, minus 650 newtons, divided by 2100 kilograms, giving 11 meters per second squared. This is not one quarter of the acceleration but all four rockets are going as we calculated in example 4.2 because the friction force is the same here. We don't have one quarter of the friction force. We have the same friction force as we did before.