Question
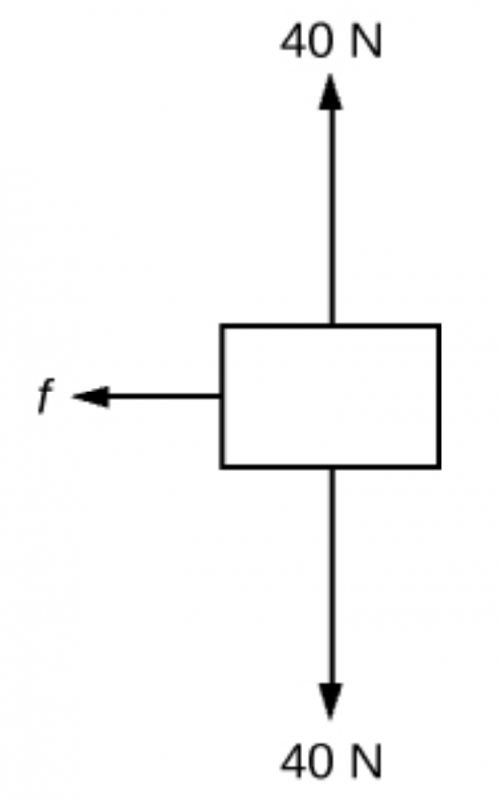
The figure shows the forces exerted on a block that is sliding on a horizontal surface: the gravitational force of 40 N, the 40 N normal force exerted by the surface, and a frictional force exerted to the left. The coefficient of friction between the block and the surface is 0.20. The acceleration of the block is most nearly
- to the right
- to the left
- to the right
- to the left
Final Answer
(d)
Solution video
OpenStax College Physics for AP® Courses, Chapter 4, Problem 28 (Test Prep for AP® Courses)

vote with a rating of
votes with an average rating of
.
Video Transcript
This is College Physics Answers with Shaun Dychko. This block experiences gravity downwards of 40 newtons, a normal force upwards of 40 newtons, and a friction force to left that we have to find. The coefficient of friction is 0.2 and we know that friction force then is this coefficient of friction multiplied by the normal force. That is 0.2 times 40 newtons, which is 8.0 newtons. Now, if we consider the x-direction, we can solve this Newton's second law for the acceleration because that's what we want to find here. We'll say that the net force in the x-direction is mass times acceleration in the x-direction. Then we also notice that the net force is the friction force horizontally. That means the friction force can be substituted in place of the net force and it equals mass times acceleration. In which case, we solve for acceleration by dividing both sides by m. So acceleration is friction divided by mass. Now we don't know what the mass is. We do know what friction is, we found that already. But let's consider the y-direction in order to determine m. The net force in the y-direction is zero because there's no acceleration vertically, it's sliding on a horizontal surface here. We can say that the net force is also the up forces minus the down forces. Since these all equals zero, we can get mg on one side here, and then divide both sides by g, and we get the m is the normal force divided by g. We substitute F N divided by g in place of m in this acceleration formula, but I'm not going to write a fraction underneath a fraction. I don't want to write this F N divided by g in the denominator of this fraction because that just gets confusing having fractions with fractions. Instead, I'm going to multiply by the reciprocal of this denominator. I'm going to multiply by the reciprocal of m. That is to say flip this fraction. We have the friction force, multiplied by g over F N. That's my substitution for m. That is 8 newtons times about 10 meters per second squared. We don't need to use 9.8 because it says is most nearly and these are all numbers with zero in the tenths place, so I'm going to put in 10 meters per second squared here for acceleration due to gravity, divided by the normal force of 40. This is 80 on top divided by 40 is is 2.0 meters per second squared. It's in the direction of the friction which is to the left so the answer is D.