Question
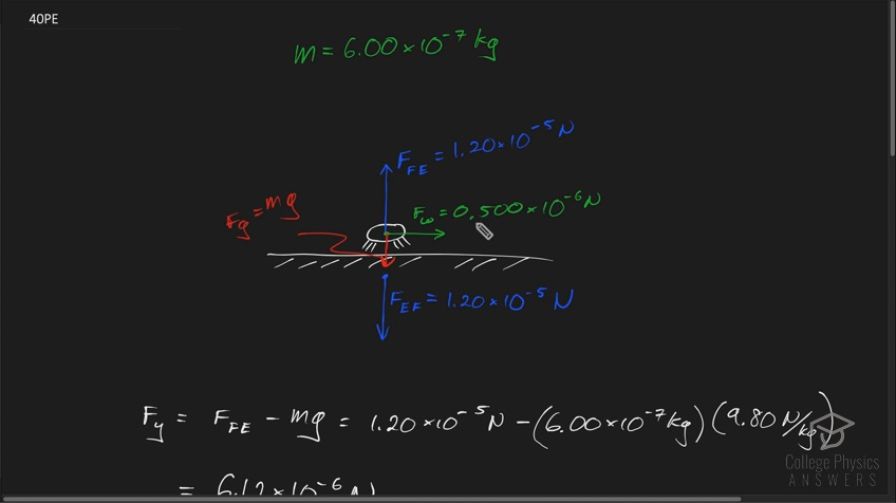
A flea jumps by exerting a force of straight down on the ground. A breeze blowing on the flea parallel to the ground exerts a force of on the flea. Find the direction and magnitude of the acceleration of the flea if its mass is . Do not neglect the gravitational force.
Final Answer
above direction of the wind.
Note: The solution video ends with finding the net force on the flea. I forgot to make the final step in calculating the acceleration, which is to divide the net force be the mass. .
Solution video
OpenStax College Physics for AP® Courses, Chapter 4, Problem 40 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
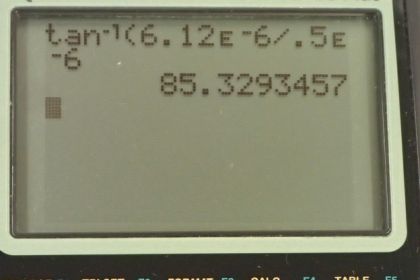
Video Transcript
This is College Physics Answers with Shaun Dychko. A flea has some wind blowing on it, which is directed parallel to the ground with a magnitude of .5 times ten to the minus six newtons. And that flea is also exerting a force on the ground. So this is the force on the, well I’ve labeled it e for earth, force on the earth due to the flea of 1.2 times ten to the minus five newtons. And in order to draw our free body diagram of the flea, we’ll need to also write the third law counterpart to this force on the flea. So the force the flea exerts on the earth is going to be in turn exerted back on the flea in the opposite direction. So we have this force on the flea due to the earth; 1.2 times seven minus five newtons directed upwards. And there’s also gravity pulling down on the flea with magnitude mass of the flea times gravitational field strength g. And the mass of the flea is given to us. What is the net force on the flea, is the question. Okay, lets get there. So, we’re going to figure out the y-component of the resultant of adding this blue, green, and red vector together. And then we’ll get the x-component as well for the resultant. The x-component is straightforward. It’s going to be only this forced due to the wind. That's the only vector that has any component in the x-direction. I guess we should draw our coordinate system here; y-positive upwards, x-positive to the right. And we have the y-component, we have the force exerted on the flea due to the earth, minus the force of gravity. And, so that's whats everything here. So, it’s 1.2 times ten to the minus five newtons, minus the mass of the flea, multiplied by gravitational field strength, giving a y-component of the resultant of 6.12 times ten to the minus six newtons. And the x-component of the resultant is the force due to the wind. And so the magnitude of the resultant is going to be the Pythagorean sum of the x and y-components. So that is the square root of the x-component squared plus the y-component squared; And so that’s .5 times ten to the minus six newtons squared. Plus 6.12 times ten to the minus six newton meters squared. All square rooted, giving 6.14 times ten to the minus six newtons. Now, that's not our final answer because that’s only the magnitude of the net force. We also need to know it’s direction. And so just to draw a picture of what we've got here; We have some y-component of the resultant, some net y-component when you take away gravity from the force exerted on the flea due to the earth. Then we have some x-component which is the force exerted by the wind. And the vector we’re determining right now has a length of 6.14 times ten to the minus six newtons. And then now we’re going to find it’s angle theta. And that is the angle above the direction of the wind. So we’re going to calculate it by, you know we can project this y-component on this side of the triangle. And we see that the y-component is the opposite and the x-component is the adjacent. And so this angle theta will be the inverse tangent of this opposite divided by the adjacent. So, it’s the inverse tangent of f y i over f x; So that’s inverse tangent of 6.12 times ten to the minus six newtons, divided by .5 times ten to the minus six newtons, giving us 85.3 degrees. So we combine these two sub-answers into the full final answer. The net force on the flea is 6.14 times ten to the minus six newtons directed 85.3 degrees above the direction of the wind.