Question
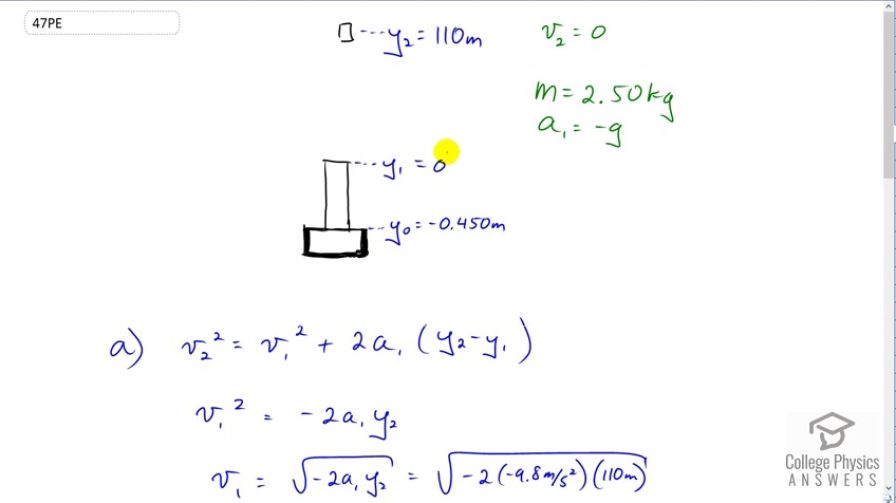
Integrated Concepts: A 2.50-kg fireworks shell is fired straight up from a mortar and reaches a height of 110 m. (a) Neglecting air resistance (a poor assumption, but we will make it for this example), calculate the shell’s velocity when it leaves the mortar. (b) The mortar itself is a tube 0.450 m long. Calculate the average acceleration of the shell in the tube as it goes from zero to the velocity found in (a). (c) What is the average force on the shell in the mortar? Express your answer in newtons and as a ratio to the weight of the shell.
Final Answer
a)
b)
c) , which is 244 times the shell's weight. (Note that 245 is written in the video, but as the calculator screenshot shows, this should be rounded to 244.)
Solution video
OpenStax College Physics for AP® Courses, Chapter 4, Problem 47 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. This mortar shoots the firework straight up into the air to a height of 110 meters which we'll take as being measured above the top of the mortar. So we'll take the top of the mortar as being y subscript one which we'll call zero meters. Then this final height of the firework then is y two, which is 110 meters and y naught we'll take to be the initial position of the firework before it is fired. That's going to be 0.45 meters below zero so that makes it negative 0.45 meters. The reason we need these three subscripts -- normally we just have y with no subscript and then a y naught because there are only two different positions to consider, the starting and the end point. But in this question there are three positions to consider and there are different accelerations in different intervals of displacements here. So, and here there is an acceleration due to gravity, and in here there is an acceleration due to the explosion of the gunpowder, whatever it is that is exploding inside this mortar to push the firework out. So, the speed at the very top here is zero because any projectile at the very top of its arc is going to have a vertical component of its velocity equal to zero. Its mass we're told is 2.5 kilograms and the acceleration which I've labeled number one for this interval here, is going to be that due to gravity directed downwards so there is a negative. So in part A, we have to figure out what is the muzzle velocity so to speak of this mortar, at what speed is the firework leaving the end of the mortar. So that is v one that we're going to be finding. So we have that v two squared is v one squared plus two times the acceleration, multiplied by the displacement which is y two minus y one . v two we know is zero and y one we've taken as a reference level so it is zero as well. Then we subtract the 2a one y two from both sides and switch the sides around so that we have v one squared equals negative 2a one y two. Then take the square root of both sides and we have the muzzle velocity of the mortar is the square root of negative two, times a one y two. So that's the square root of negative two, times negative 9.8 meters per second because that's the acceleration that the mortar experiences after it leaves -- sorry, the firework experiences after it leaves the mortar, multiplied by 110 meters and that gives 46.4 meters per second. Now what acceleration did the firework experience in this tube is the next question. We'll use the same kinematics formula but now we have different subscripts because we're talking about different positions here. So the velocity at position one, is what we have just calculated in part A and that squared equals the velocity at the very initial position squared, and that is going to be zero when it's down here at position zero. Add to that two times the acceleration during this interval here of displacement and we call that a naught times y one minus y naught. We'll solve this for a naught by well, switching the sides around and also noticing that y naught is zero. Then we have -- sorry, did I say that right? No I didn't say that right. y naught is negative 0.450 meters. Often we have y naught equal to zero but today we have y one equal to zero. So, we have y one equal to zero here. So we have two a naught times negative y naught equals v one squared. So I switched the sides around as well because we want the unknown on the left, and then divide both sides by negative two y naught. We have a naught then is negative v one squared over two y naught. So that is negative 46.4327 meters per second and we square that and the negative sign is outside of the square so this numerator remains negative despite this square here. Then divide by two times negative 0.45 meters which gives positive 2.40 times ten to the three meters per second squared as the acceleration the firework experiences within the tube of the mortar. Then we calculate the force on the firework, and by force I assume that they mean net force, and so that is mass times acceleration. So we take the 2.5 kilogram mass that we're given, times the acceleration we just calculated with some more digits here because we want to avoid intermediate rounding error. We don't want to use a rounded number in a calculation and we divide by -- sorry, we multiply those two and we get 5.99 times ten to the three newtons is the force on the firework. The weight of it is mass times the gravitational field strength. So that's 2.5 kilograms times 9.8 which is 24.5 newtons and the ratio of those two forces, the net force to the weight, is 245. So the net force the firework experiences is 245 times its weight.

