Question
(a) What is the initial acceleration of a rocket that has a mass of 1.50 \times 10^6 \textrm{ kg}2.00 \times 10^6 \textrm{ N}$? Do not neglect gravity. (b) What is unreasonable about the result? (This result has been unintentionally achieved by several real rockets.) (c) Which premise is unreasonable, or which premises are inconsistent? (You may find it useful to compare this problem to the rocket problem earlier in this section.)
Final Answer
a)
b) The rocket is accelerating down instead of up.
c) The thrust is not large enough, or the mass is too large.
Solution video
OpenStax College Physics for AP® Courses, Chapter 4, Problem 39 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
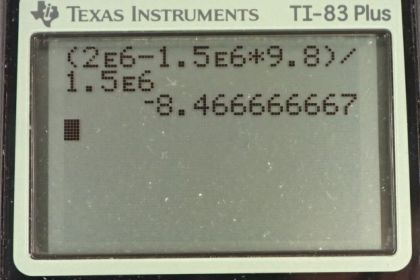
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. We are told that the thrusters on this rocket will propel it upwards with a force of 2.00 times ten to the six newtons and there's also gravity pulling it backwards with a magnitude mg. We're given the mass of 1.5 times ten to the six kilograms. So the question is what will the acceleration of the rocket be? Well, the net force is going to be the thrust force upwards minus the weight downwards and that equals mass time acceleration. Then we'll divide both sides by m to solve for a and also switch the sides around. So we have acceleration is the thrust force minus force of gravity divided by mass and substituting mg in for force of gravity there, we have 2.00 times ten to the six newtons minus 1.5 times ten to the six kilograms times 9.8 meters per kilogram, a ll divided by the mass of 1.5 times ten to the six. This gives us negative 8.47 meters per second squared. So this is unreasonable because the rocket is accelerating downwards instead of up and we expect rockets to accelerate upwards. This is the result from the fact that the thrust is maybe not large enough or the mass is too large.