Question
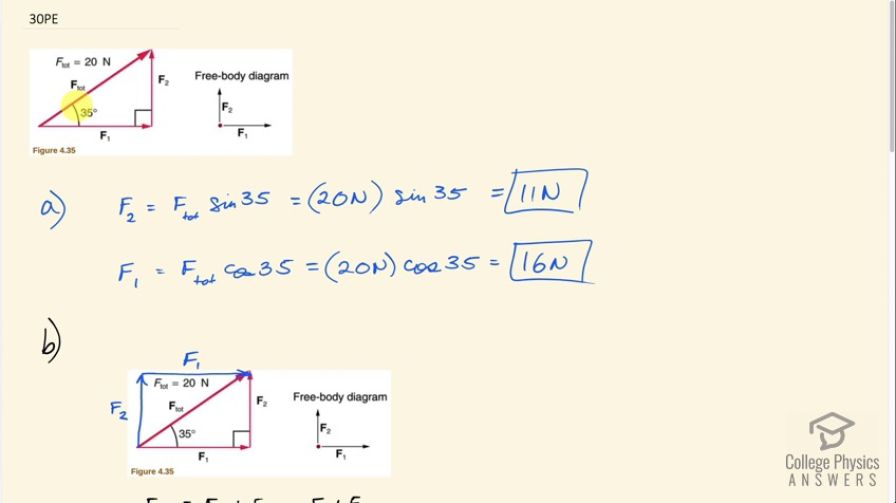
(a) Find the magnitudes of the forces and that
add to give the total force shown in Figure 4.35. This
may be done either graphically or by using trigonometry. (b) Show graphically that the same total force is obtained independent of the order of addition of and . (c) Find the direction and magnitude of some other pair of vectors that add to give . Draw these to scale on the same drawing used in part (b) or a similar picture.
Final Answer
- ,
Please see the solution video for parts (b) and (c).
Solution video
OpenStax College Physics for AP® Courses, Chapter 4, Problem 30 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
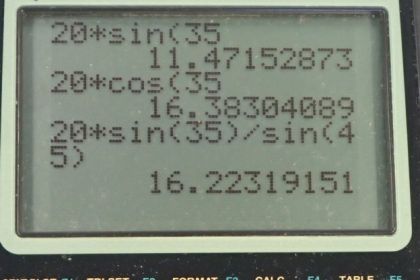
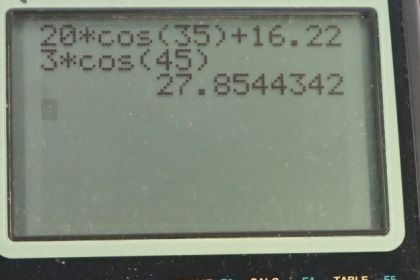
This is College Physics Answers with Shaun Dychko. Given this picture where we have a total resultant vector of length 20 newtons, 35 degrees above the x-axis. We have to figure out what these components are. This horizontal vector f one and this vertical vector f two. So f two will be this hypotenuse f total multiplied by sine of 35, because it’s the side opposite to this given angle. And that’s 20 newtons times sine 35, which is 11 newtons. f one is the adjacent leg of this right triangle. And so it is 20 newtons times cosine 35, which is 16 newtons. In part B we show that if you change the order of adding f one and f two, you end up with the same resultant. So whereas before we had f one beginning at the origin and then travel along f two, in blue I’m showing that we can begin with f two at the origin. And then add f one. And we end up at the same final position. So it’s the same resultant vector in other words. So f two plus f one equals f one plus f two so addition of vectors, commute, is the fancy math word. Okay, and that comes from the word commuting, like in a car going to work. Commuting is moving around and so you can move around terms when you're adding and you end up with the same answer. Okay, so part C, we have to just invent two different vectors that add up to the same resultant. And so I have f one labeled with an apostrophe which we call prime. f one prime is going to be along here. And then f two prime is going to be at an angle 45 degrees above the negative x-axis. Because it’s going to the left. And it’ll end up at the same final position. And we have to figure out what these two vectors are. So the total x-component of the resultant has to be f one prime. Which is positive to the right and completely to the right. So there’s no need for any trig function here. Minus f two prime times cosine 45. Because this is the adjacent leg of this little bit of f two prime here. f two prime x-component is here and that's gonna equal the f total times cos 35. That's the total x-component of this resultant. And then there’s nothing we can do with that anymore, because we don't know what f one prime nor f two prime are. So we have two unknowns in this equation and we can’t solve it, but if you have a second equation then you can. So we have the y-component of the resultant equals the y-component of f one prime, which is zero. Plus the y-component of f two prime which is f two prime times sine 35 or 45 I should say. And that equals the y-component of the resultant, which is f total times sine 35. And then we can solve for f two prime by dividing both sides by sine 45. And we get then that f two prime is 20 newtons times sine 35 divided by sine 45, which is 16 newtons. Then we can return our attention to this equation for the x-direction, solving for f one prime by adding f two prime cos 45 to both sides. And we get f one prime. Then is f total times cos 35, plus f two prime times cos 45. That’s 20 newtons times cos 35 plus 16.223 newtons times cos 45, which is 28 newtons. So our final answer is that f two prime is 16 newtons, 45 degrees above the negative x-axis, which means it’s up and to the left. And then f one prime is 28 newtons to the right.