Figure 4.42 represents a racetrack with semicircular sections connected by straight sections. Each section has length d, and markers along the track are spaced d/4 apart. Two people drive cars counterclockwise around the track, as shown. Car X goes around the curves at constant speed _v_c, increases speed at constant acceleration for half of each straight section to reach a maximum speed of 2_v_c, then brakes at constant acceleration for the other half of each straight section to return to speed _v_c. Car Y also goes around the curves at constant speed _v_c, increases its speed at constant acceleration for one-fourth of each straight section to reach the same maximum speed 2_v_c, stays at that speed for half of each straight section, then brakes at constant acceleration for the remaining fourth of each straight section to return to speed _v_c.
(a) On the figures below, draw an arrow showing the direction of the net force on each of the cars at the positions noted by the dots. If the net force is zero at any position, label the dot with 0. Description of Figure 4.43:
(a) The first dot on the left center of the track is at the same position as it is on the Car X track.
(b) The second dot is just slight to the right of the Car X dot (less than a dash) past three perpendicular hash marks moving to the right.
(c) The third dot is about one and two-thirds perpendicular hash marks to the right of the center top perpendicular has mark.
(d) The fourth dot is in the same position as the Car X figure (one perpendicular hash mark above the center right perpendicular hash mark).
(e) The fifth dot is about one and two-third perpendicular hash marks to the right of the center bottom perpendicular hash mark.
(f) The sixth dot is in the same position as the Car Y dot (one and two third perpendicular hash marks to the left of the center bottom hash mark).
(b) i. Indicate which car, if either, completes one trip around the track in less time, and justify your answer qualitatively without using equations.
ii. Justify your answer about which car, if either, completes one trip around the track in less time quantitatively with appropriate equations.

Video Transcript

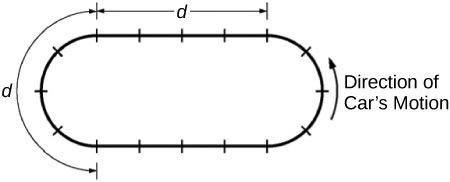
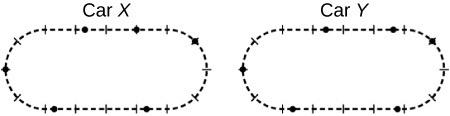
This is College Physics Answers with Shaun Dychko. Going around a curve at constant speed does require some acceleration because the direction of the velocity is changing. So at this point despite the constant speed, the car is accelerating towards the center of this radius of curvature here. So towards the center of the circle would make up this curve, and likewise here, going constant speed in this curved portion requires an acceleration towards the center which is perpendicular to the velocity. For car Y, you have the same explanation for these two arrows there. Now, car X accelerates during the first half of a straight section, and so this dot is in the first half and so the acceleration is to the right because it is speeding up. Likewise for this dot, for the same reason it is speeding up there and accelerating to the right. Up here, it's just at the beginning of this section here and so this dot requires an arrow to the left because it is speeding up there. It's traveling in this direction by the way. This last dot it is slowing down here so it requires a force pointing, opposing the direction of motion and causing a negative acceleration if you like, or an acceleration that's in the opposite direction to its velocity. So it's an arrow pointing to the right here. Now for car Y, this dot here is at the one quarter mark if you ask me, of this section, and so at that point it stops accelerating because it has reached its final top speed. Then it'll continue that top speed until it gets to the three quarter mark. So there's no acceleration and therefore no force required, no net force. For this dot here, it reached the three quarter mark in this straight section and so it is decelerating and it will have a force directed in the opposite direction to its velocity. Then this dot here is at the one quarter mark and so it has finished accelerating and is now at its top speed. This one looks to me like it's at the three quarter mark of this section here and, well, actually if it was at the three quarter mark you would need to start decelerating. This is maybe more in the middle actually. So being in the middle, it's cruising at constant speed during the middle portion of this section. All right. So, and yeah, by the way, the text that describes more precisely where this dot is, says that it is one and two thirds perpendicular hash marks to the right of the bottom center. So here is the bottom center hash mark and it is one and two thirds to the right of that. So that means it is two thirds this way in this section which places it in the middle half. If it was one and three quarters, then it would be just finishing its acceleration. But being only one and two thirds, means it is definitely within the constant speed portion of that section. Okay. So, qualitatively we can say that car Y will complete the round trip in less time than car X because it spends more time at its top speed because it's finished accelerating by time it gets to the one quarter mark and then spends half of the straight section at top speed; whereas car X spends only brief instant of time at top speed at the halfway mark before it begins decelerating again towards the end of the straight section. Then the curved sections are equal for both cars because they both go at constant speed. So because car Y spends more time at top speed in the straight section that means it will spend less time completing the track. Now, doing that with formulas, well, we're going to find out the total time it takes car X to go around the track and both, we'll consider just one straight section which has a length of d over 4 because our figure here says that d is the distance of four sections and so when we consider one straight section that's one quarter d. There are two time intervals to consider for car X, the time interval during which it is accelerating up to its top speed here and then the time interval when it is decelerating from the mid-point to the end of the section. So, this distance here is half of d over 4 which is d over 8 and that's going to be the average velocity multiplied by the time. The average velocity will be vc at the start plus two vc we're told is the final velocity and all that divided by two and then multiplied by delta t x one. Then collect those two like terms, you get three vc times delta t x one over two equals d over 8, switching sides around as well there. Then multiply both sides by two over three vc to solve for which will be d over 12 vc. Delta t x two is going to be a similar story. It's also d over 8 for this section here and then it starts at two vc is its initial speed at this midpoint, and ends at vc at the end of this section, all divided by two and it's all the same number, just a different order of the terms there. So the answer will be the same as for delta t x one. So the total time to do one section between perpendicular hash marks, is going to be delta t x one plus delta t x two which is basically two times d over 12 vc which is d over six vc. So the total time around the entire track, will be two d over vc because there is a -- this distance d here and then this distance d here on the curved portions, and the time to do each of them is d over vc because it goes at constant speed vc over each of these curved portions. There is two of them so two times d over vc plus eight of these little sections, straight sections that we just calculated the time for. So there's one, two, three, four, five, six, seven, eight, and then so that's eight times delta t x. Substituting for delta t x is d over 6 vc. We have two d over vc plus four d over three vc then making a common denominator by multiplying top and bottom of this fraction by three, we get 6d over three vc and that gives a total of ten d over three vc is the time for car X to complete one lap. Then we've car Y to consider and there are four sections, sorry, there is three time intervals to consider for one straight section. There is the time interval during which it is accelerating, delta t y one, there's the -- and that occurs over a distance of d over 16 so that's the one quarter mark of a straight section and a straight section is of distance d over 4, so a quarter of d over 4 is d over 16. Then we have half of this straight section which is d over 8, during which the car is going at constant speed, a top speed of two vc. Then again we have another section delta t y three when the car is slowing down from two vc back to its speed of vc. Okay. So, the total time for this straight section will be delta t y one plus delta t y two plus delta t y three and so let's figure out where each of them are. So this distance here d over 16, is going to be the average velocity during that time interval, multiplied by the time interval. So it starts at vc and it ends at two vc here and I'l' divide that sum by two, and then multiply that by delta t y one and collect the like terms at the top to get three vc delta t y one over two equals d over 16. Then multiply both sides by two over three vc and this gives delta t y one is d over 24 vc. This middle section here which has a distance of d over 8, is going at constant speed and the speed is two vc and that's getting multiplied by delta t y two which we then solve for by dividing both sides by two vc. This gives us d over 16 vc is delta t y two. Delta t y three is the same numbers as for finding delta t y one but just a different order of the terms in the numerator there because it starts at two vc and it ends at speed of vc. So the` answer will be the same for delta t y three as it was for delta t y one, d over 24 vc. So adding those together, we have two times d over 24 vc plus d over 16 vc. That means d over 12 vc plus d over 16 vc and then getting a common denominator of 48 vc, we end up with four d over 48 vc plus three d over 48 vc which is seven d over 48 vc. So that's the time for one straight section for car Y. Then the total time to do the entire lap for car Y, is going to be two d over vc which accounts for the constant speed curved portions just as we had for car X, plus eight times these straight section times. So that's eight times seven d over 48 vc. So that makes two d over vc plus seven d over six vc and 48 divided by eight being six, and a common denominator of six vc is called for, so we have 12 d over six vc plus seven d over six vc which is nineteen d over six vc. So we need to compare that to t x now. So t x we found before is 10 d over three vc, found that here, and to make the comparison easier let's make a common denominator. So that's twenty d over six vc when you multiply top and bottom by two. So we can see that the total time for car Y being nineteen d over six vc is less than the total time for car X which is twenty d over six vc.