Question
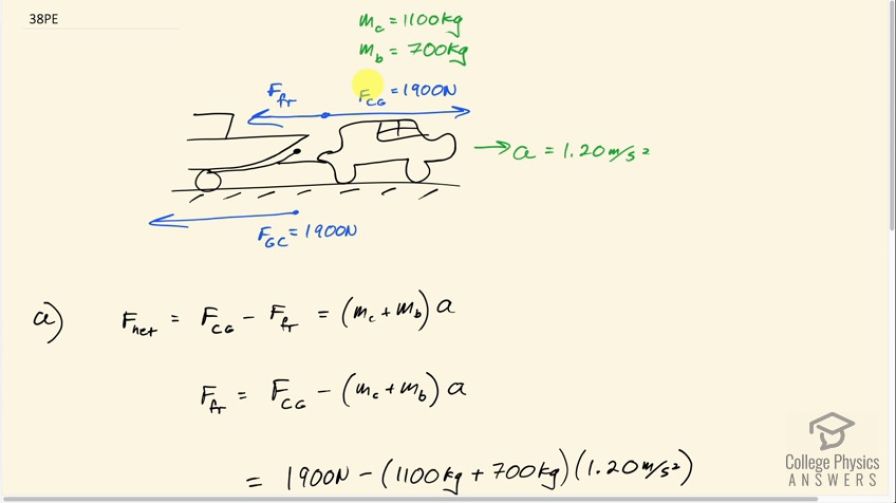
A 1100-kg car pulls a boat on a trailer. (a) What total force resists the motion of the car, boat, and trailer, if the car exerts a 1900-N force on the road and produces an acceleration of ? The mass of the boat plus trailer is 700 kg. (b) What is unreasonable about the result? (c) Which premise is unreasonable, and why is it unreasonable?
Final Answer
- The friction force is in the direction of motion. This is not possible.
- The acceleration can not be this large with only a 1900 N force from the car.
Solution video
OpenStax College Physics for AP® Courses, Chapter 4, Problem 38 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. A car of mass 1100 kilograms is pulling a boat and trailer which has a combined mass of 700 kilograms. And the car applies a force on the ground due to the car of 1900 newtons. Which tells us what the force on the car due to the ground is, because that’s the Newton’s third law counterpart. It’s the same magnitude as 1900 newtons but in the opposite direction going forwards. The acceleration we’re told to assume is 1.20 meters per second squared. Although we’ll find out later that this is an unreasonably high number. And our job is to figure out what is this force of friction opposing the motion. So the net force is the force to the right, which is the force on the car due to the ground. Minus the force to the left, which is friction, and that equals the total mass of car and boat-trailer combined, times by the acceleration. So we can solve for the friction force by moving it to the right hand side. And then moving this to the left hand side and then switching the sides around. And we get to the friction force, is the force on the car due to the ground, minus mass of the car plus mass of the boat times acceleration. So it’s 1900 newtons minus 1100 kilograms plus 700 times 1.2 m per second squared, which is negative 260 newtons. And now the way I write down Newton’s second law as I write down these forces, with the assumption that the numbers I’m going to plug-in are always positive. And then negative signs indicate direction, I write explicitly in the formula. So I wrote a minus here because the friction force is drawn to the left, in the negative direction. We’re taking right to be positive. So if we get a negative answer that means that the force is in the opposite direction to what has been drawn. That might be a bit confusing, but this negative does not say it’s to the left in the way we have our method here. These numbers are meant to be positive. And so if we get a negative that means that we’ve drawn our arrows the wrong way. And so this friction force is the opposite to what has been drawn, which means it is to the right. And that is not reasonable because friction forces cannot be in the direction of motion. And so the premised that’s unreasonable is that the acceleration is 1.3 meters per second squared given only 1900 newton force from the car.
