Question
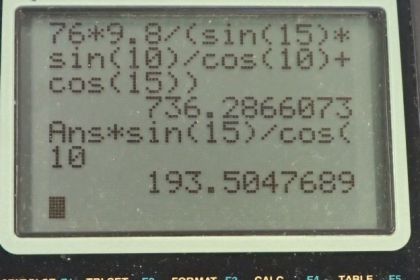
A 76.0-kg person is being pulled away from a burning building as shown in Figure 4.41. Calculate the tension in the two ropes if the person is momentarily motionless. Include a free-body diagram in your solution.
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 4, Problem 42 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
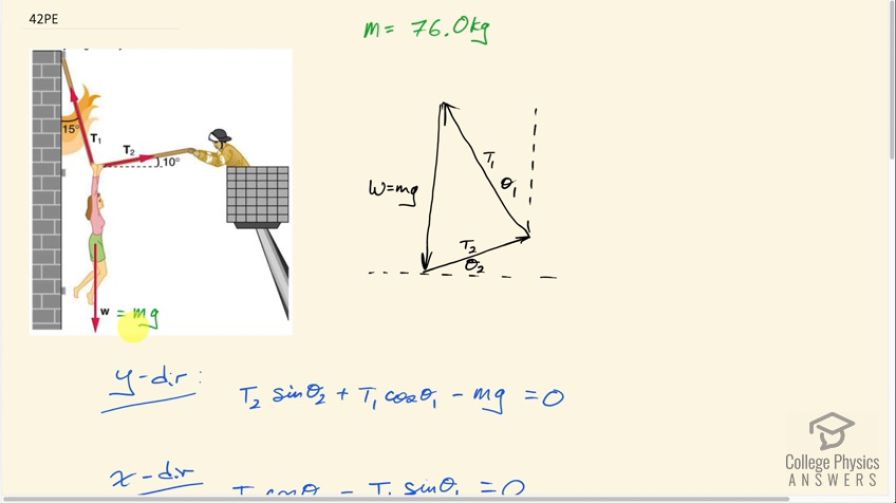
This is College Physics Answers with Shaun Dychko. We’re going to calculate the tension in each of these segments of rope, given that this woman is hanging with a weight equal to her mass, times acceleration due to gravity. And this tension has to add up to zero when combined with the weight. So the total force on this woman, because she’s stationary, has to add up to zero. So we have this tension two pulling in this direction along this rope. And we put the tail of tension one on the head of tension two vector. And in that tension one is up like this with this angle theta one, 15 degrees with respect to the vertical. This here is 15 degrees as well, because these are interior opposite angles between two parallel lines. So that’s 15 degrees here and this one is 10 degrees. And we have then the tail of the weight vector straight down, and ends up at the place where we started. Because they add up to zero. So we’ll consider the y-direction and we’ll take the y-component of the tension two force which is this opposite segment here. This is t two y. And because it’s the opposite segment, we will take sine of this angle and multiply it by the hypotenuse t two. And then the y-component of t one will be this leg here, which is adjacent to the angle theta one. So, t one y gets multiplied by cosine of theta one to get it’s y-component. Both of those are positive because they’re upwards and then minus this weight which is entirely in the y-direction downwards m g and all that equals zero. Because there’s no acceleration, that equals m a, but I just substituted zero for a to make this zero. Okay, and in the x-direction, we have the x-component of tension two which is the adjacent leg of this right triangle. And, so we use cosine of theta two times t two to find it. And then that's in the positive direction. So that makes it a positive here and then tension one has a x-component in the negative direction. So we put a minus t one times sine theta one. Because this is the opposite leg of this triangle. And all of that equals mass times acceleration, but acceleration being zero and just put zero here. Now we have two equations and two unknowns t two and t one. So well solve this x-direction equation for t two, and we’ll add t one sine theta one to both sides. And then divide both sides by cosine theta two and we end-up with t two equals t one sine theta one over cos theta two. And this is useful because now we can substitute this into our y-direction equation and replace t two with all of this. And now we have a single equation with only one unknown, which is t one. So this is the y-direction equation rewritten with t two replaced in red with this expression here. So we can factor out t one from both of these two terms and we get t one times bracket, sine theta one times sine theta two, over cos theta two plus cos theta one. And then we add m g to both sides. And we get m g on the right hand side here. And then we divide both sides by this bracket to solve for t one. So, t one is m g over all of the stuff; So that’s 76 kilograms times 9.8 newtons per kilogram divided by sine of 15 degrees. Times sine of 10 degrees, divided by cosine of 10 degrees, plus cosine of 15 degrees. So theta one is 15 and theta two is 10. This works out to 736 newtons. Now tension two then we can return to this expression here tension two is tension one that we just found times sine theta one over cos theta two. So we have this 736.287 newtons times sine 15 over cos 10, gives 194 newtons.