Question
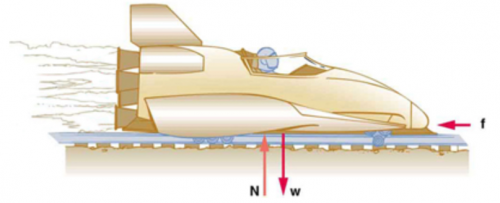
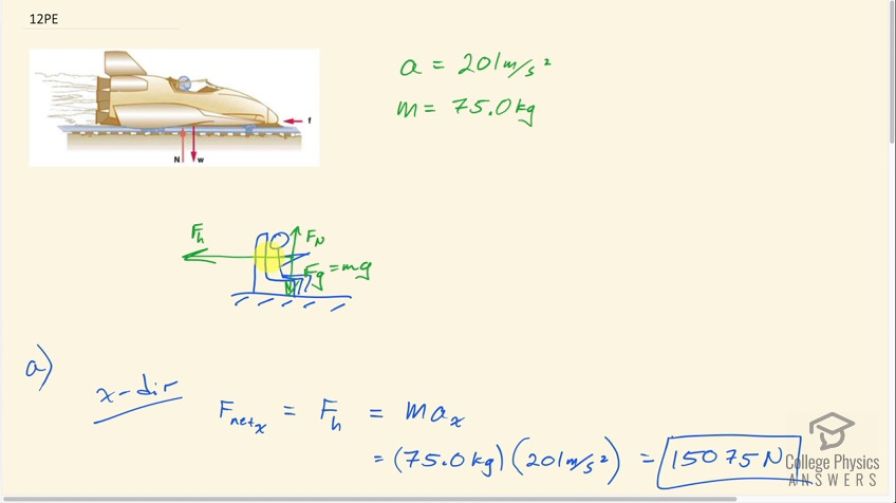
The rocket sled shown in Figure 4.33 decelerates at a rate of . Its passenger has a mass of 75.0 kg. (a) Calculate the horizontal component of the force the seat exerts against his body. Compare this with his weight by using a ratio. (b) Calculate the direction and magnitude of the total force the seat exerts against his body. In this problem, the forces are exerted by the seat and restraining belts.
Final Answer
- . This force is 20.5 times the passenger's weight.
Solution video
OpenStax College Physics for AP® Courses, Chapter 4, Problem 12 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
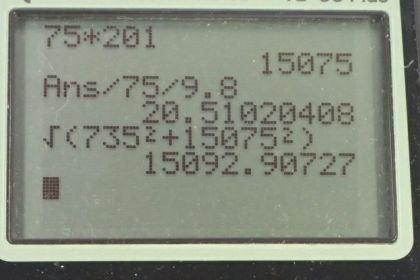
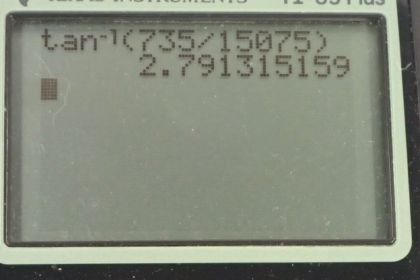
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. This passenger and the rocket sled experiences a normal force upwards due to the seat and a horizontal force due to the seat belt going backwards. They're also going to experience the force of gravity downwards due to the earth but it's just these two forces here that are exerted by the seat. This normal force and this horizontal force will be combined in Part B into a resultant force by the seat and well find its direction, but one thing at a time. First, we want to consider just the x-direction. We know that the net force in the x-direction equals the horizontal force because there are no other forces acting horizontally. That force is always mass times acceleration because that's Newton's second law, and we have the x-component of the acceleration here. That is 75 kilograms mass of the person times 201 meters per second squared acceleration which is 15,075 newtons. Now finding this horizontal force as a ratio of the person's weight, we go horizontal force divided by m g. That's 15,075 newtons divided by 75 kilograms times 9.8 newtons per kilogram, and that is 20.5 times their weight. In Part B, we figure out what is this vertical force due to the seat. That's normal force, in other words. The vertical net force is the mass times the vertical acceleration, but they're not accelerating vertically at all. So we have zero here. We can also write this vertical net force as the normal force upwards minus the force of gravity downwards. Substituting mg in place of force of gravity, and then add mg to this side and mg to this side, then we say normal force equals the weight. So 75 kilograms times 9.8, which is 735 newtons. Now the total force exerted by the seat then will be the Pythagorean some of this normal force upwards and the horizontal force. This is a right triangle and we're finding the length of its hypotenuse by taking the square of each side and adding and then square rooting that sum. We have the square root of 735 newtons squared, plus 15,075 newtons squared, which gives 1.51 times 10 to the 4 newtons. That's the total force exerted by the seat on the person. The direction of this force will be the inverse tangent of the opposite divided by the adjacent. This normal force is opposite to the angle theta, and this horizontal force is adjacent to that angle. We can find it by going inverse tangent of 735 newtons divided by 15,075 newtons. That makes this angle 2.80 degrees and that is above the negative x-axis where we've defined to the right to be positive here.