Question
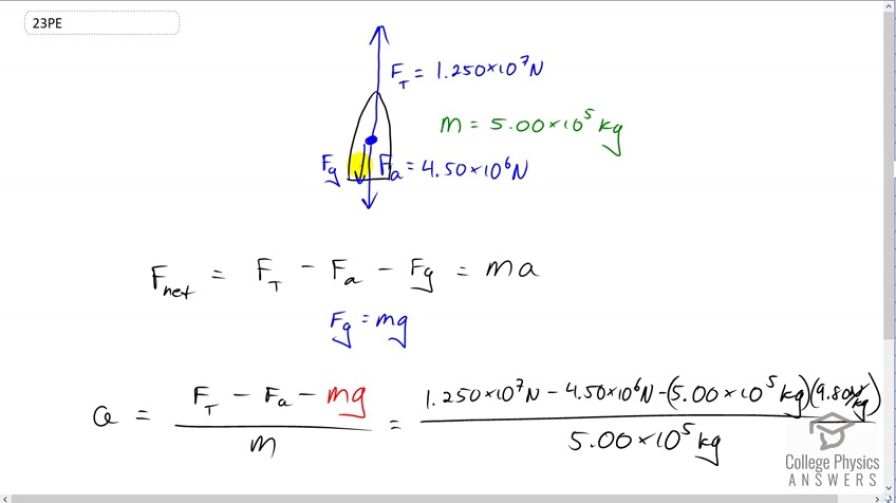
A rocket is accelerating straight up. Its engines produce of thrust, and air resistance is . What is the rocket’s acceleration? Explicitly show how you follow the steps in the Problem-Solving Strategy for Newton’s laws of motion.
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 4, Problem 23 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. One of the best ways to prepare any of your solutions is to draw a picture. So that's what I've done here. This is especially important for forces or dynamics questions because you need to draw the free body diagram to show all the forces involved. So with this rocket we have a thrust force upwards of 1.25 times ten to the seven newtons and then downwards we have gravity and then we also have the air resistance which is directed opposite to the direction of motion and so that will be downwards as well because the rocket is moving up. So the air friction down is 4.5 times ten to the six newtons. We're told that the mass of the rocket is 5 times ten to the five kilograms and so we've drawn a free body diagram and written down everything that we know. Then we can proceed to the algebra which is that the net force is the up force, up forces minus the down forces, and so we have up as the thrust force and then minus each of the down forces, air and gravity. That net force equals mass times acceleration. Gravity is mg. So we'll divide both sides by m here and then substitute for fg and we get this line here, acceleration is thrust, minus air resistance, minus mg weight, divided by the mass, m. We substitute each of those numbers in here and we end up with 6.2 meters per second squared as the acceleration of the rocket.
