Question
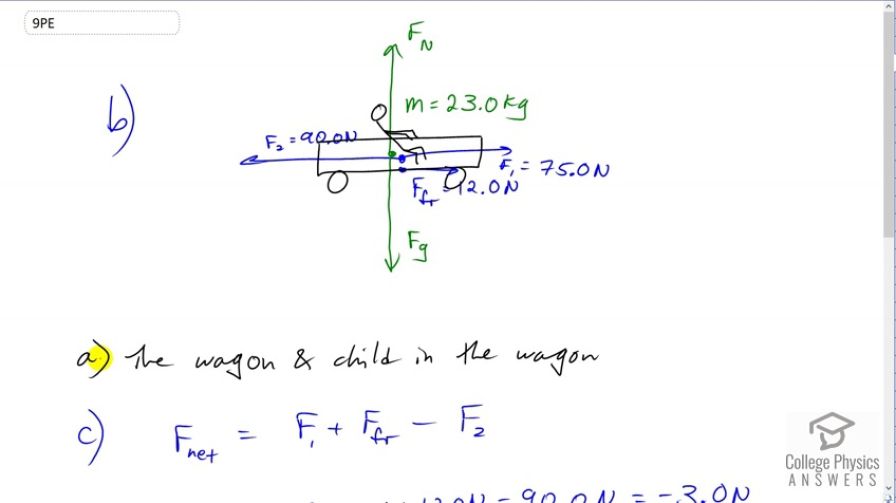
Suppose two children push horizontally, but in exactly opposite directions, on a third child in a wagon. The first child exerts a force of 75.0 N, the second a force of 90.0 N, friction is 12.0 N, and the mass of the third child plus wagon is 23.0 kg. (a) What is the system of interest if the acceleration of the child in the wagon is to be calculated? (b) Draw a free-body diagram, including all forces acting on the system. (c) Calculate the acceleration. (d) What would the acceleration be if friction were 15.0 N?
Final Answer
a) The wagon and the child in the wagon compose the system of interest.
b) see video
c)
d) 0
Solution video
OpenStax College Physics for AP® Courses, Chapter 4, Problem 9 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College physics Answers with Shaun Dychko. I am going to answer part B first by drawing a free body diagram of the system. Although I guess -- well, let's answer part A first. The system is the wagon and the child which is in the wagon. The other children which are pushing the wagon are not drawn here because they're not the thing moving. They're the things that are applying the forces and those forces are drawn here. Those forces are on this wagon and child in the wagon system. So we have the force one, force exerted by child one of 75 newtons to the right, so we assume child one is over here pushing on the wagon, that's child number one. Then we have child two on the right side pushing towards the left, 90 newtons. There is the force of friction and there's a bit of a question what direction should that friction go? Well friction always opposes motion and so because this force is bigger than this one, we know that the wagon is going to accelerate to the left and it's going to be moving to the left in other words. So, we know that because it's accelerating to the left that's how the direction it will move only because we're told it starts at rest. So now we have friction that will oppose that motion. So, I was kind of making a point there that this friction does not always point in the opposite direction of the acceleration, by the way. It's -- in a different type of trickier question, they could have said the wagon was already moving to the right in which case for sure friction would re-point it to the left even if this friction or this force two is bigger causing an acceleration to the left. If the thing was moving to the right, then the friction would be pointing to the left. Okay. So, this wagon not moving at all from the start, here are the forces, it must be accelerating to the left in other words, and moving to the left. So the friction is to the right. All right. Then we draw the normal force and the force of gravity. They're not very interesting because they are equal and opposite directions and so the wagon will not accelerate vertically. So the net force, horizontally speaking of course, is the force one to the right, plus the friction force also to the right, minus the force applied by child two to the left. So that's 75 newtons plus 12 newtons minus 90 which makes negative 3 newtons. Then acceleration is that net force divided by mass. So we take this net force divide it by the 23 kilograms, combined mass of the child and wagon, and that gives negative 0.13 meters per second squared. Now we can't really answer this question with a negative or positive -- I mean we could but it's even better to answer it in terms of the position of the children because somebody else could have drawn this picture with child one on this side pointing to the left and child two on this side exerting a force to the right. So in order to be not ambiguous, we'll say 0.13 meters per second squared towards child one, whatever side they happen to be on. Then in part D, what if the friction force was 15 newtons? That would mean there is no net force, therefore no acceleration and this must be a static friction force because there'd be no motion either.
