Question
Integrated Concepts: A basketball player jumps straight up for a ball. To do this, he lowers his body 0.300 m and then accelerates through this distance by forcefully straightening his legs. This player leaves the floor with a vertical velocity sufficient to carry him 0.900 m above the floor. (a) Calculate his velocity when he leaves the floor. (b) Calculate his acceleration while he is straightening his legs. He goes from zero to the velocity found in part (a) in a distance of 0.300 m. (c) Calculate the force he exerts on the floor to do this, given that his mass is 110 kg.
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 4, Problem 46 (Problems & Exercises)
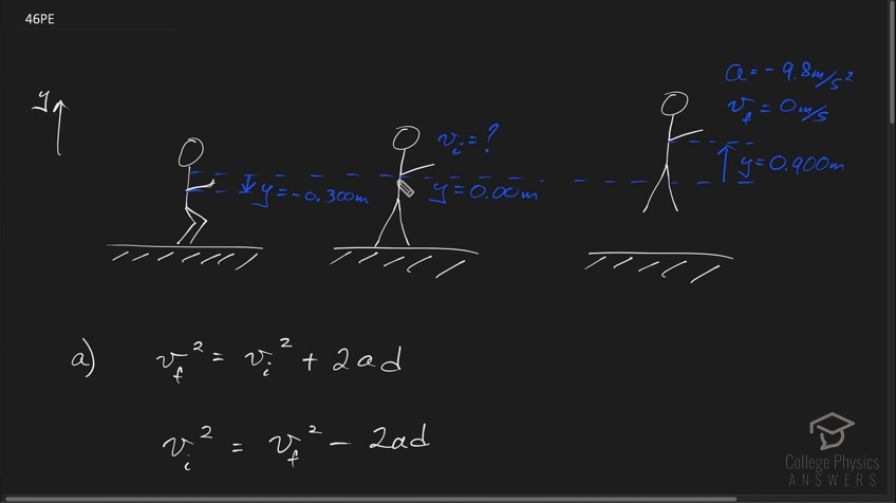
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. A basketball player crouches down 0.3 meters and then accelerates upwards in order to launch himself 0.9 meters into the air, that's 0.9 meters above the ground. I've taken this point where his shoulder is, where his arms meet his body to be the point to which I measure, and then straight up standing position will be the zero level. When he's crouched down, the position of his shoulder is going to be negative 0.3 meters. Then once he jumps up, the shoulder will be positioned at 0.9 meters positive. Now when he's in the air, he has an acceleration of negative 9.8 meters per second squared as everything does on the surface of the earth, neglecting friction of course. At the very peak of his leap, his velocity will be zero. The final is zero meters per second at the very top of the jump. When he's standing straight up, this is just before his feet leave the ground. At this point, we need to know what this velocity will be. That's the answer to part A. Then when he's crouch down, we want to know what the acceleration is assuming that it's constant, beginning at this crouch position, ending at this standing position, what acceleration does he give himself. Then Part C is what force is he exerting on the floor. Now here's our one of our kinematic equations. It says the final velocity squared is initial velocity squared plus two times acceleration times displacement. I'm referring to this picture from here to here. There's an initial velocity that we don't know, a final velocity of zero, and the acceleration we know, and the displacement we also know. We can rearrange the two sides. I mean, I just said this was zero, so I guess we can just make that zero as well, zero. We're going to subtract 2adfrom both sides and then switch the sides around the unknown, the initials on the left. If the initial squared equals negative 2ad, then we'll take the square root of both sides. We have initial velocity then is the square root of negative 2ad. That's a square root of negative two times negative 9.8 meters per second squared times the displacement of positive 0.9 meters, giving 4.20 meters per second is his initial velocity right here. This is 4.20 meters per second. Then part B is, what is the acceleration? Well, I'm using this kinematics equation again. But I'm putting little prime symbols as a superscript just to make sure there's no confusion with the same symbols used in part A because the V final here is not the same as the V final here, because in Part B, we're considering the period of time between the crouch position to the standing position. The initial velocity here is zero when he's crouched. I forgot the primes there. he final velocity is what we calculated in part A, and we want to figure out what the acceleration is which will be different than the acceleration when he was in the air since this is the acceleration of gravity here, but when he's crouched and then exerting a force in order to stand up and then leap, this acceleration will not be the acceleration due to gravity. We will subtract the initial prime squared from both sides and then also divide both sides by 2 times final y position minus initial y position that is the widest placement in other words. Then we solve for the acceleration during this time period, which we call a prime. So that's 4.2 meters per second squared divided by two times the final position of zero right here, minus an initial position of negative 0.3 meters. That's the position here. This works out to 29.4 meters per second squared. Then finally, in part C, we want to know what force is exerted on the floor due to the player. Well, we can figure out what the force on the player due the floor is and then we'll say that the force on the floor to the player is the Newton's third law counterpart to the force on the player to the floor. The negative of it in other words. One step at a time, we're told that the player's mass is 110 kilograms, and we know that the force on the player to the floor upwards positive, minus the force of gravity downwards, the mass of the player times gravitational field strength equals the mass of the player times the acceleration. This is Newton's second law. Then we'll add mg to both sides in order to solve for F pF and also factor out the common factor m here. We have m times a plus g is going to be the force on the player to the floor. It's 110 kilograms times 29.4 meters per second squared acceleration that we calculated in part B plus 9.8 meters per second squared, acceleration due to gravity, getting a force of 4,310 newtons upwards. Now the force on the floor due to the player is going to be the negative of that. That is negative 4,310 newtons.
