Question
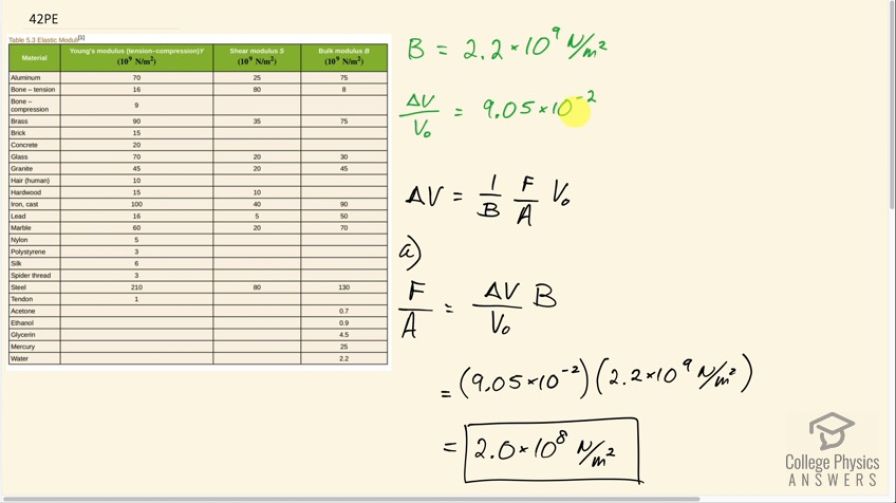
(a) When water freezes, its volume increases by 9.05% (that is, ). What force per unit area is water capable of exerting on a container when it freezes? (It is acceptable to use the bulk modulus of water in this problem.) (b) Is it surprising that such forces can fracture engine blocks, boulders, and the like?
Final Answer
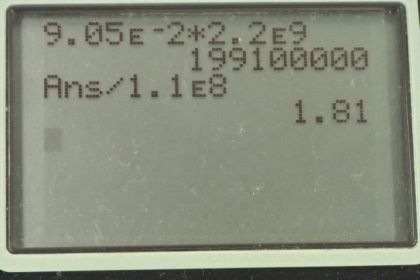
- The pressure of freezing water is greater than the highest pressure in the ocean, at the bottom of the Mariana Trench, by a factor of 1.8. It is no surprise that freezing water can crack strong materials.
Solution video
OpenStax College Physics, Chapter 5, Problem 42 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. When water freezes, it has a fractional change in volume of 9.05 times 10 to the minus 2 and that is ΔV over V naught in other words. So this is the change in volume divided by the original volume. So we are going to also look up the Bulk modulus for water which is 2.2 times 10 to the 9 newtons per square meter— that's for water— and we'll use this formula to solve for the pressure which is force divided by area and we'll do that by multiplying both sides by Bulk modulus over the original volume and so we have the pressure then is the fractional change in volume multiplied by the Bulk modulus. And that is 9.05 times 10 to the minus 2 times 2.2 times 10 to the 9 newtons per square meter which is 2.0 times 10 to the 8 newtons per square meter. Now to decide whether or not that's a big number, let's use the pressure at the bottom of the Mariana trench— which is the deepest part of the ocean— as a point of comparison and that pressure I looked up in Google is 1.1 times 10 to the 8 newtons per square meter. And so the pressure of water freezing divided by the pressure at the bottom of the Mariana trench is 2.0 times 10 to the 8 over 1.1 times 10 to the 8 which is 1.8. So the pressure of freezing water is greater than the highest possible pressure in the ocean by a factor of almost 2 so it's no surprise that freezing water can crack strong materials.