Question
Calculate the maximum acceleration of a car that is heading up a slope (one that makes an angle of with the horizontal) under the following road conditions. Assume that only half the weight of the car is supported by the two drive wheels and that the coefficient of static friction is involved—that is, the tires are not allowed to slip during the acceleration. (Ignore rolling.) (a) On dry concrete. (b) On wet concrete. (c) On ice, assuming that , the same as for shoes on ice.
Final Answer
Solution video
OpenStax College Physics, Chapter 5, Problem 14 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
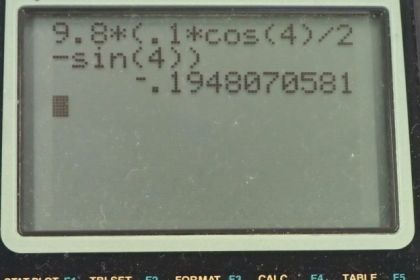
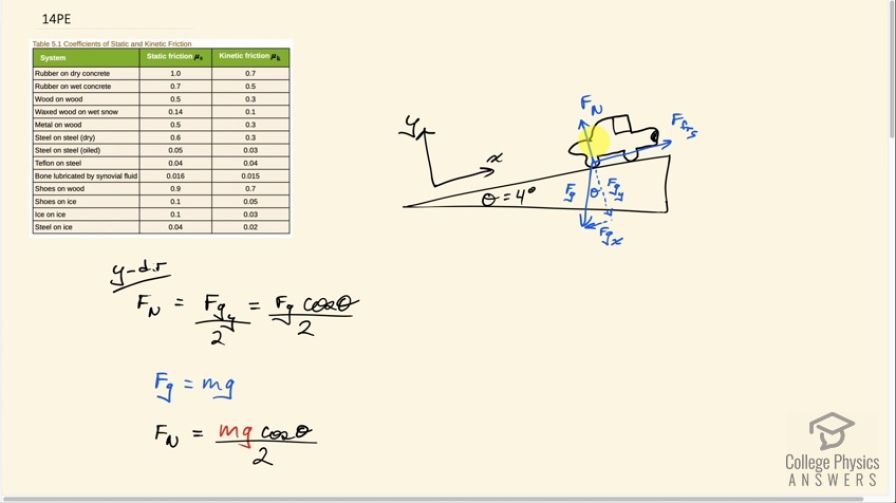
This is College Physics Answers with Shaun Dychko. This car is trying to get up this slope and it has an angle of 4 degrees and we assume that only half of the car's weight is being supported by the driving wheels and the driving wheels is where all of the static friction force applied by the ground on the wheels will be applied because they are the driving wheels and they are the ones that are applying a force backwards on the ground and then the ground has a Newton's third law counterpart pushing those wheels forwards. We need to figure out what this normal force is to calculate what the static friction force is and then eventually solve for the acceleration of the car. Let's first turn our attention to that normal force: we can say that the normal force equals half of the total gravity that's perpendicular to the slope. Notice that we have aligned our coordinate system so that x is positive up the slope and the y-axis is perpendicular to the slope and I have tried to intentionally draw this normal force about half the length of this y-component of gravity to indicate that this wheel experiences only half of the total weight and I suppose for completeness, I can put another normal force on these wheels. Okay! So we have that F g y over 2 then is the normal force and then this y-component of gravity is the adjacent leg of this right triangle— and when I say right triangle, I mean there's a right angle here— and being the adjacent leg then we use cos of Θ multiplied by this hypotenuse which is mg—the force of gravity— to calculate this component here. And so you know, we substitute mg in place of F g and we have the normal force then is mg times cos Θ all divided by 2 since the two driving wheels support only half of the weight. In the x-direction, we can say that the static friction force up the slope minus the component of gravity that is down the slope, F g x, equals mass times acceleration and then we can make substitution's for each of these terms here. The maximum static friction force is the coefficient of static friction multiplied by the normal force and then we can substitute the normal force that we figured out when we considered the y-direction in here so that's μ smgcos Θ over 2 and then for the x-direction of gravity, it's gonna be the opposite leg of this triangle and so we use sin Θ multiplied by this hypotenuse to get it. I notice that there's no divide by 2 business here because this gravity is acting on the entire car. Okay! So we have mg times sin Θ is the x-component of gravity. So substituting into this expression here, this Newton's second law, we have that the static friction force, which is μ smgcos Θ over 2, minus the x-component of gravity, which is mgsin Θ, equals mass times acceleration. So we can divide both sides by m, switch the sides around to isolate a on the left side and then factor out the common factor g. So we have acceleration then is acceleration due to gravity times μ scos Θ over 2 minus sin Θ. So then in parts (a), (b) and (c), we substitute in different values for the coefficient of static friction. So in part (a), we are told to assume that we have rubber on dry concrete so we look in table [5.1] for rubber on dry concrete and the static friction coefficient is 1.0. So we plug in 1.0 here for μ s, cos 4 degrees divided by 2 minus sin 4 degrees and multiply all that by 9.8 meters per second squared and we get an acceleration of 4.2 meters per second squared that is up the slope. In part (b), we have rubber on wet concrete and looking that up in this table, the static friction coefficient is 0.7. So all these numbers are the same as in part (a) except we have 0.7 instead of 1.0 and we get an acceleration of 2.7 meters per second squared. In part (c), we are told that the slope is icy and that the coefficient of static friction is 0.100. So we plug that in and we find that our answer is negative 0.195 meters per second squared; this negative sign indicates that the car will be accelerating down the slope and will not be able to climb this hill.
Comments
In your free body diagram, wouldn't static friction be faced the opposite direction given that friction opposes motion?
Kinetic friction opposes motion. Static friction is what's acting between the tires and ground since there isn't skidding. Yes, the car is moving, and yes the tires are rolling, but with a narrow view of just the contact patch between the ground and tires, there isn't motion. The contact patch descends until it touches the ground, then lifts off. While touching the ground, static friction between the contact patch and ground pushes the ground backwards, and the ground in turn pushes the contact patch (and thus the attached tire, wheel, and car) forwards.