Question
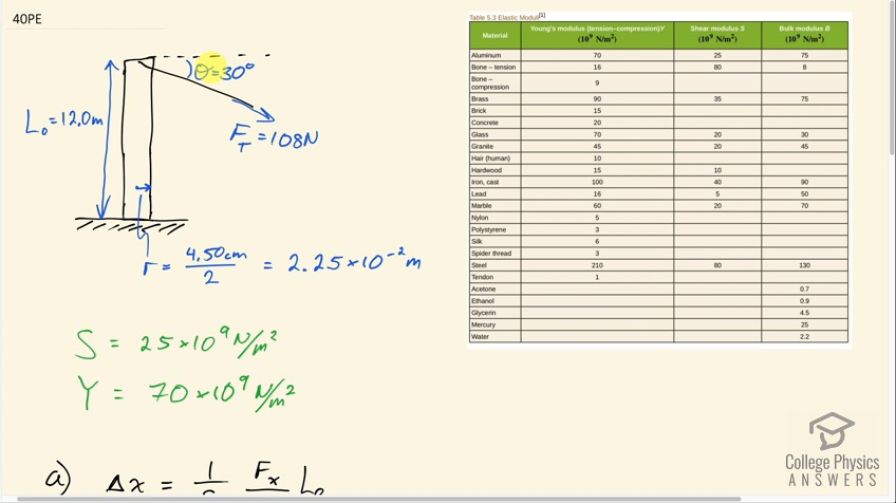
To consider the effect of wires hung on poles, we take data from Example 4.8, in which tensions in wires supporting a traffic light were calculated. The left wire made an angle below the horizontal with the top of its pole and carried a tension of 108 N. The 12.0 m tall hollow aluminum pole is equivalent in stiffness to a 4.50 cm diameter solid cylinder. (a) How far is it bent to the side? (b) By how much is it compressed?
Final Answer
Solution video
OpenStax College Physics, Chapter 5, Problem 40 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. There's a cable on the top of this aluminum pole pulling with a tension force of 108 newtons at an angle of 30 degrees below horizontal; it's attached at the top of the pole and the pole is 12 meters high and we assume that it has it's equivalent to a solid aluminum rod with a diameter of 4.5 centimeters. We are gonna divide that by 2 to get the radius since that's what we are going to use for our cross-sectional area formula π times radius squared. So I divide the diameter by 2 and then also take care of the unit conversions into meters by multiplying by 10 to the minus 2 meters. So information we'll need for part (a), we are asked the shear deformation or the sideways displacement and that's going to require the shear modulus which we look up for aluminum— it is 25 times 10 to the 9 newtons per square meter— and then when we calculate the compression of this pole, we'll need to know the Young's modulus which is 70 times 10 to the 9 newtons per square meter for aluminum. So in part (a), the amount of sideways displacement is gonna be 1 over the shear modulus times the x-component of this tension force and we divide that by the cross-sectional equivalent area times the length. So the x-component is going to be the adjacent leg of this triangle here; if we break this tension force into components: this is the adjacent leg and so that means we need to multiply the hypotenuse by cos of the angle. So F T times cos 30 degrees gives F T x. I have just been writing F x but I guess F T x might be a little bit more precise. Okay! And the area is πr squared so we make substitutions for each of those here and then we plug in numbers. So the shear deformation is 1 over 25 times 10 to the 9 newtons per square meter— shear modulus— times 108 newtons times cos 30 divided by π times 2.25 times 10 to the minus 2 meters squared times 12 meters giving us 2.8 times 10 to the minus 5 meters. So it's not gonna be tipped over by any perceptible amount; you need very precise measuring devices to notice that. Now the amount of compression is going to be the y-component of that tension force times the length of the pole divided by its Young's modulus times the cross-sectional area. So the y-component is the opposite leg of this triangle so we need to go sin Θ times the hypotenuse. So that's sin Θ times F T and then the area is still πr squared and so we substitute for both of those, F y and A, and then plug in numbers. So 108 newtons times sin 30 times 12.0 meters over 70 times 10 to the 9 newtons per square meter—Young's modulus— times π times 2.25 times 10 to the minus 2 meters squared gives 5.8 micrometers of compression.
