Question
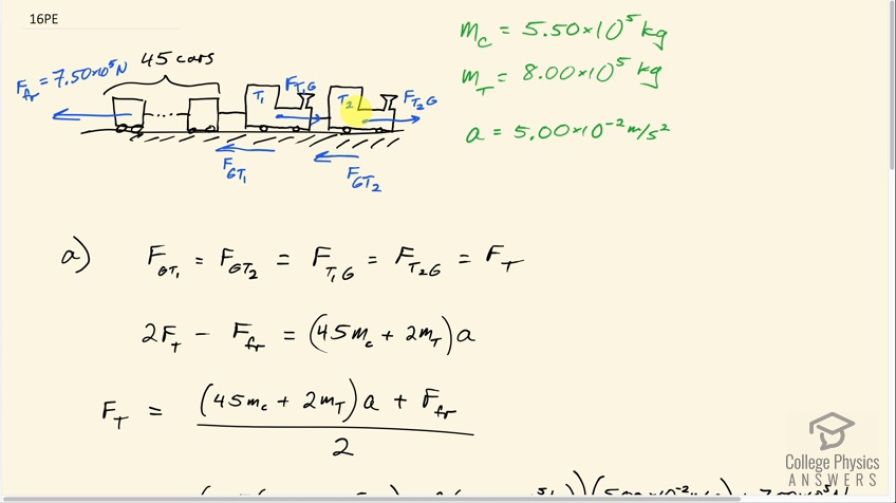
A freight train consists of two engines and 45 cars with average masses of . (a) What force must each engine exert backward on the track to accelerate the train at a rate of if the force of friction is , assuming the engines exert identical forces? This is not a large frictional force for such a massive system. Rolling friction for trains is small, and consequently trains are very energy-efficient transportation systems. (b) What is the magnitude of the force in the coupling between the 37th and 38th cars (this is the force each exerts on the other), assuming all cars have the same mass and that friction is evenly distributed among all of the cars and engines?
Final Answer
Solution video
OpenStax College Physics, Chapter 5, Problem 16 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. We have two engines each of which has a mass of 8 times 10 to the 5 kilograms and those engines are exerting a force backwards on the ground. So this is the force on the ground due to train engine one and this is the force on the ground due to train two and there's a Newton's third law reaction force on each of the trains due to the ground corresponding to each of these forces on the ground due to the respective trains. And so there are in total two forces pushing this entire train forwards: there's a force on engine one and there's a force on engine two and we assume that they are of equal size. So you know, I could have drawn this a bit more simply I suppose but since the question asks for the force on the ground, I wanted to show explicitly how that relates to forces that are on the train. Okay! So if we can find the force that's on the train then that will be the force on the ground because all these forces are equal to each other and let's just call that F T for "train" I guess; I could have used the letter "E" for engine actually but anyway we are stuck with the letter "T" here. So we have two engines and so we have two times the force of one of them; that's the total force to the right and opposing that is this friction force which is to the left and that's the total friction on all the forty-five cars plus two engines and then we are given that number here and all of that has to equal the total mass times the acceleration of the system. So the total mass is 45 times the mass of a single car plus 2 times the mass of a single train engine and our job is to solve for F T. So we'll rearrange this Newton's second law by adding force of friction to both sides and then divide both sides by 2 and we solve for the force exerted by a train. I almost said tension there... anyway, we'll get to tension in part (b) when we talk about the coupling in the last eight cars. So the force on a single engine is 45 times the mass of a single car plus 2 times the mass of a single engine times acceleration plus the force of friction all divided by 2. So that is 45 times 5.50 times 10 to the 5 kilograms plus 2 times 8.00 times 10 to the 5 kilograms times the acceleration of 5.00 times 10 to the minus 2 meters per second squared plus this friction force all divided by 2 which is 1.03 times 10 to the 6 newtons— that is the force that's being exerted by the ground on a single train car and is therefore the force that that train car in turn exerts on the ground. Okay! In part (b), we imagine that there's a tension force in the coupling between the 37th and 38th car. So thirty-seven of the car's don't matter and there's a total of forty-five of them so the total mass... this box represents a whole bunch of cars all put together how many is the question right now and the answer to that is 45 in total minus the 37 that are on the right hand side of this coupling for a total of 8 on the left hand side. So there are eight cars that are being accelerated by this particular coupling between the 37th and the 38th car. So the total mass of these tail cars that are on the tail end of the train is 8 times a single car. So there's some friction opposing the motion of these last eight cars and I gave it a little prime symbol here to distinguish it from the friction that is here... this is the total friction on all of the elements of the train— that being forty-five cars and two train engines— and so we are told that the friction is distributed evenly among all the elements and there are 47 elements— 45 cars plus 2 engines— and here we have 8 elements in this package here and so our friction force is gonna be 8 divided by 47 times the total friction given to us in part (a). So Newton's second law then can be set up as this coupling force that we have to find, F T, minus the friction force prime and that equals the total mass of these 8 cars times acceleration. So we'll add this friction force to both sides well, I suppose this F T could use a prime as well couldn't it because it's not the same as this F T up here... this is the force in this coupling. Okay! So this friction is the same friction as up here though by the way. (where were we) We are adding friction prime to both sides and now we are solving for F T prime— this force on the coupling between the 37th and the 38th car. It's gonna equal the total mass of the tail here times its acceleration plus this friction force prime. So that is 8 cars times the mass of a single car times the acceleration and the acceleration is the same as before— it's all accelerating together— plus 8/47th times the total friction on the entire train. So that's 8 times 5.50 times 10 to the 5 kilograms times 5.00 times 10 to the minus 2 meters per second squared plus 8/47th times 7.50 times 10 to the 5 newtons which is 3.48 times 10 to the 5 newtons.
