Solution video
OpenStax College Physics, Chapter 5, Problem 21 (Problems & Exercises)
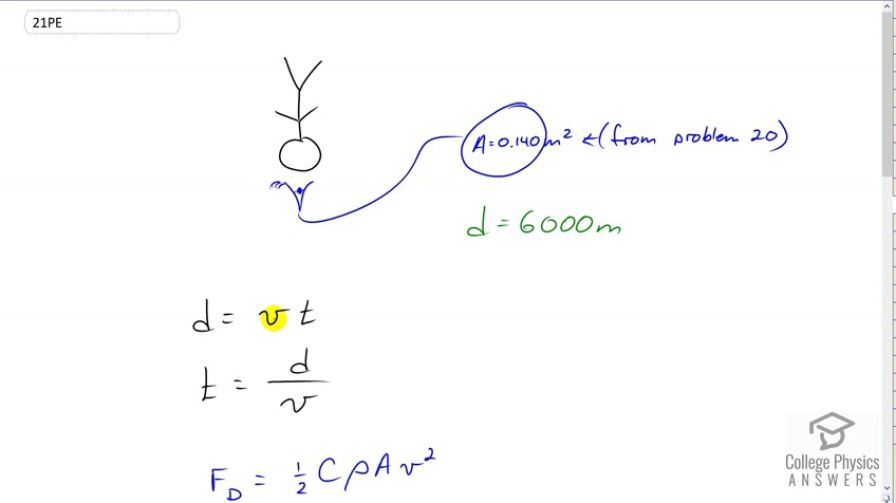
Calculator Screenshots
Comments
I'm a bit confused about this one. The problem says that the time is small to reach terminal velocity, but it does not say that it is not ignorable . Does your answer mean that if a question gives us a quantity that is small, we should ignore it?
Thank you for your question openD,
There isn't going to be a strict rule to follow in this area. "Small" is often a clue that yes, we can ignore it, as we did here. It's important to consider the context. In this problem we're making an assumption about the cross-sectional area of the skydiver. Right away we know there is considerable error in whatever calculation we do since there will be significant error in that assumption. Would considering the small time to reach terminal velocity adjust our answer significantly? By analogy, would considering the time to reach terminal velocity be like "adding milimeters to an answer in kilometers"? If the kilometers were measured with an exceptional device that has an error of milimeters or less, than this would be appropriate. However, adding milimeters to the kilometers on a traffic sign giving the distance to the next city would be inappropriate. So, with this in mind, the answer to your question is, "it depends". Remember that physics is not math class, which is to say that real world considerations of error need to be brought to bear.
Hope that helps,
Shaun


