Solution video
OpenStax College Physics, Chapter 5, Problem 29 (Problems & Exercises)
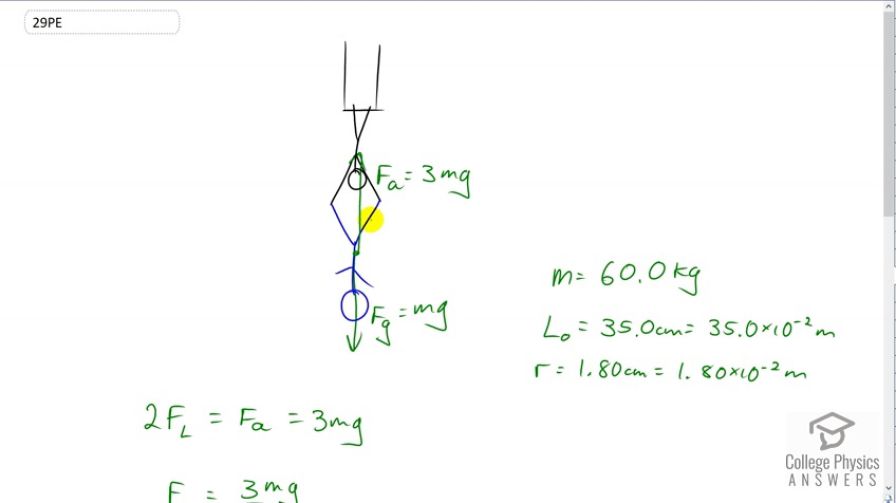
Calculator Screenshots
Comments
30. During a wrestling match, a 150 kg wrestler briefly stands
on one hand during a maneuver designed to perplex his
already moribund adversary. By how much does the upper
arm bone shorten in length? The bone can be represented by
a uniform rod 38.0 cm in length and 2.10 cm in radius
so i have a question. on your calculator entry, you have entered for the last entry, 35x10^-2 / π /1.8x10^-2 ²
shouldnt pi be multiplied by r². it appears that you have divided it.
Hi Michael,
Thank you for the question. You're quite right that gets multiplied by in the denominator. Nevertheless, the calculator screenshot is correct, as written. I could have done 35x10^2 / ( π x 1.8x10 -2 ²) with brackets, which is what I think you were expecting. Expressions are always evaluated from left to right, while keeping BEDMAS in mind. With 35x10^-2 / π /1.8x10^-2 ², the 35x10^-2 is divided first by π, then then that result is divided by 1.8x10^-2 ². This works out the same as if I had used brackets in the denominator. I just have a personal preference for less button pushing, so I choose to usually avoid putting the denominator in brackets. The exception is when there is addition or subtraction in the denominator, in which case the brackets are necessary to ensure that the sum or difference is calculated first (the "B" in BEDMAS) before dividing.
All the best,
Shaun


