OpenStax College Physics, Chapter 5, Problem 20 (Problems & Exercises)

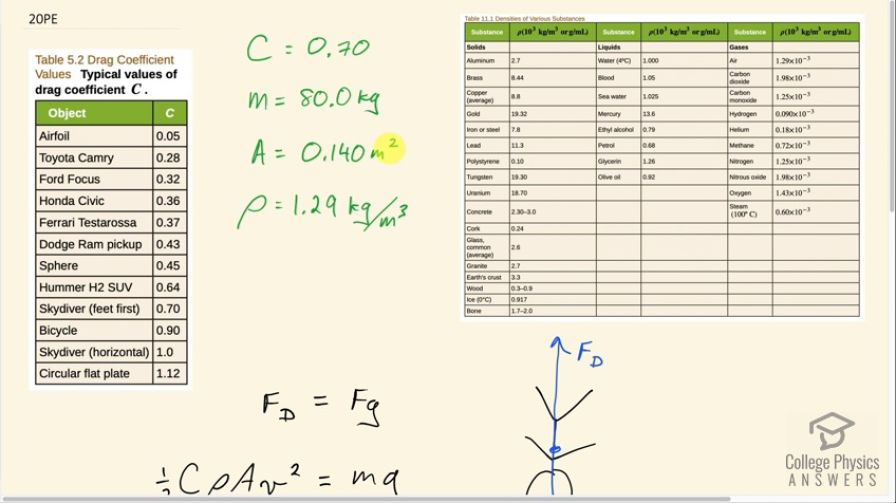
This is College Physics Answers with Shaun Dychko. We are going to calculate the terminal velocity of a skydiver that has an area of 0.14 square meters— that's their cross-sectional area as they are falling through the air. The air has a density of 1.29 kilograms per cubic meter and I found this table in chapter 11—table [11.1]— that has the density of air and the mass of the person we are told is 80 kilograms and in table [5.2], we can find the drag coefficient of a skydiver who is feet first and we'll assume that going headfirst is the same coefficient so we'll call it 0.70. When they reach terminal velocity that means that the drag force upwards equals the weight downwards and so we can say one-half times drag coefficient times density of the air times their cross-sectional area times their velocity squared—that's the formula for drag force— equals mg and then we'll solve for v. We'll multiply both sides by 2 and divide both sides by CρA and then I'll take the square root of both sides as well and so we have then that the terminal velocity equals the square root of 2mg over drag coefficient times density times area. So that's square root of 2 times 80.0 kilograms times 9.80 newtons per kilogram divided by 0.70 times 1.29 kilograms per cubic meter times 0.140 meters squared and that gives 111.37 meters per second. And it's a bit easier to conceptualize the speed by converting it into kilometers per hour so we multiply by 3600 seconds per hour and then times by 1 kilometer for every 1000 meters and we are left with 4.0 times 10 to 2 kilometers per hour.