Question
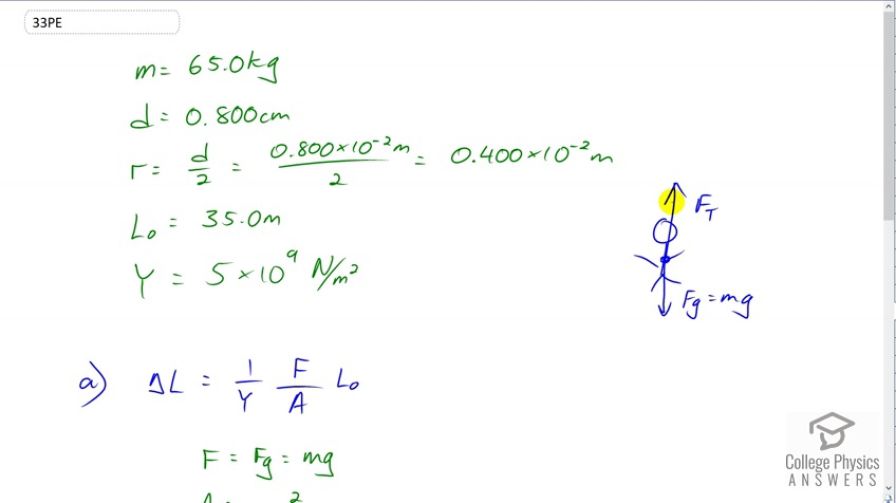
(a) By how much does a 65.0-kg mountain climber stretch her 0.800-cm diameter nylon rope when she hangs 35.0 m below a rock outcropping? (b) Does the answer seem to be consistent with what you have observed for nylon ropes? Would it make sense if the rope were actually a bungee cord?
Final Answer
a)
b) Yes, this is reasonable since a nylon rope is not meant to stretch much. A bungy cord would stretch much more.
Solution video
OpenStax College Physics, Chapter 5, Problem 33 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. A climber is hanging by her rope and we want to find out how much does the nylon stretch. So the force of tension upwards is going to equal the force of gravity downwards and so that will give us f in our formula for delta l. But before we get ahead of ourselves, let's write down all the data we're given. We know that the climber is 65.0 kilograms. The diameter of the nylon rope is 0.8 centimeters and we'll divide that by two since our formulas are going to need radius for calculating the cross sectional area of the rope. So we go diameter divided by two which is 0.8 times ten to the minus two meters, also taking care of unit conversion by writing times ten to the minus two instead of the prefix centi. Then that gives 0.4 times ten to the minus two meters for the radius. The original length of the rope is 35 meters and we're told -- actually we look it up in the data table, that the Young's Modulus for nylon is five times ten to the nine newtons per meter squared. So the change in length of the nylon is one over Young's Modulus times the force applied to stretch it, divided by its cross sectional area, times its original length. We have the force is going to be mg, the force due to gravity, and the area is pi r squared. So we make substitutions for f and a on this line here. So we have delta l is one over Young's Modulus times mg over pi r squared times l naught. So that's one over five times ten to the nine newtons per square meter, times 65 kilograms mass, times 9.8 newtons per kilogram, divided by pi times 0.4 times ten to the minus two meters radius, squared, times 35 meters original length, which gives about 9 centimeters. That does seem reasonable since a nylon rope is not meant to stretch that much but it will stretch a bit and it would not be a bungee cord because that would stretch a lot more.
