Question
(a) Calculate the acceleration of a skier heading down a slope, assuming the coefficient of friction for waxed wood on wet snow. (b) Find the angle of the slope down which this skier could coast at a constant velocity. You can neglect air resistance in both parts, and you will find the result of Exercise 5.9 to be useful. Explicitly show how you follow the steps in the Problem-Solving Strategies.
Final Answer
a)
b)
Solution video
OpenStax College Physics, Chapter 5, Problem 11 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
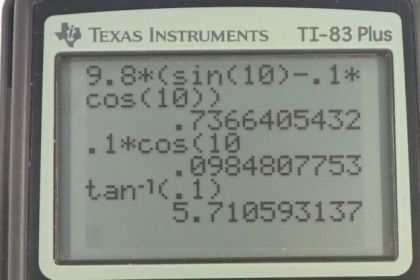
Calculator Screenshots
Video Transcript
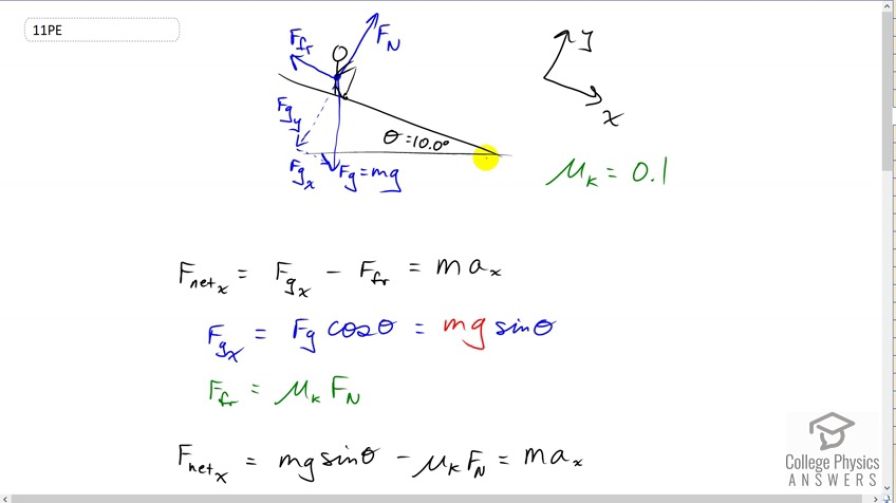
This is College Physics Answers with Shaun Dychko. We start this question by drawing a picture as we do for pretty much every question. We have a skier going down a slope that’s inclined at ten degrees. We’ve drawn a free body diagram to show the three forces on the skier. These two dotted lines arrows are the components of this force of gravity. I’ve rotated the coordinate systems so that x is going down the slope and y is going perpendicular to the slope. In the textbook, they often label the x-axis here as the parallel axis and the y-axis as the perpendicular axis, that’ll be fine too. We know that this skier is not accelerating perpendicular to this slope, so we know that this normal force equals this y component of gravity. We’ll use that normal force to multiply by the coefficient of kinetic friction between waxed wood and snow, and then that’ll give us the friction force. We have a component of gravity directed down the slope, so that’s the component in the positive x direction and then we’ll have to calculate this friction in the negative x direction to figure out the net force which is going to equal mass times acceleration in the x direction. Now we know that this angle in here is theta and you can remember that by looking at this triangle here, this is a right triangle and so this angle up in here, we’ll call alpha. Since 90 degrees of this yellow triangle are taken up by this right angle down here, that means alpha plus theta has to equal 90, because the total angles in a triangle are 180 and 90 is already accounted for there, leaving us 90 leftover for the sum of these two. Then this is a right angle here as well between Fgy and the slope and so that means alpha plus whatever this angle is here plus, well let’s pretend we don’t know what it is, we’ll call it gamma, maybe that’s a bit confusing but that has to equal 90. Now we know that this alpha is 90 minus theta from here so we can plug that in up there, it’s a bit messy sorry, hopefully it’s good enough. We have 90 minus theta plus gamma equals 90 and you can subtract 90 from both sides and then add theta to both sides and you see that gamma equals theta. So in other words, this angle in here which I was calling gamma for a moment is the same as theta. So that’s why we can say that’s theta in there. Alright. So that means Fgx is the opposite leg of this triangle here in blue and so because it’s the opposite leg we can multiply the hypotenuse Fg, force of gravity, by sin theta. Fg is mg, and so multiply mg by sin theta to get this x component of gravity down the slope. This force of friction is coefficient of kinetic friction times the normal force, and then we’re gonna substitute each of this into this formula here. We have the Fgx is mg sin theta, and we have the force of friction is mu k Fn, and all of that equals mass times acceleration in the x direction. Now that’s not quite good enough because we don’t know what the normal force is, but since we know that the net force in the y direction, perpendicular to the slope in other words, is zero. That means Fn upwards minus Fgy downwards has to equal zero and you can add Fgy to both sides and you get Fn equals Fgy. Fgy is the adjacent leg of this blue triangle and so we use cosine theta multiply by the hypotenuse Fg to get it. Substitute mg in for Fg, we have mg cos theta is the normal force. So returning back to the net force in the x direction, we have it equal to mg sin theta minus mu k times mg cos theta equals ma x. Then divide everything by m to get rid of it, and then we flip the sides around so we get a x equals g, which I factored out between these two terms, times sin theta minus mu k cos theta. Then we can plug in the numbers to get our answer for the acceleration, 9.8 meters per second squared times sine of ten degrees minus 0.1 times cosine of ten degrees, gives 0.74 meters per second squared. I have two significant figures here because if you go 0.1 multiplied by cos 10, you get 0.09 something something something, and so it’s precise to the hundreds place and that means when you’re subtracting or adding, the result of that subtraction and adding is also going to be precise to the hundreds place. That’s why I’ve rounded this to the hundreds place. Then in part b, we’re asked to find what angle of the slope will result in no acceleration. We’ve found the formula for the acceleration already so let’s reuse that, and set it to zero. And then we can divide both sides by g so that g is gone and add mu k cos theta to both sides and have sin theta equals mu k cos theta. Then divide both sides by cos theta to have only one trigonometric function, tangent, sine over cosine is tangent. So tan theta is mu k, which means theta is the inverse tangent of mu k. Inverse tangent of 0.1 is 5.7 degrees to have no acceleration and just coast at a constant speed down the slope.
Comments
For a, is it still correct if I got -0.74 m/s2? I drew my incline opposite of yours so all my signs were switched for the x and y axis.
So long as you're clear in your diagram which direction is positive, then it should be fine. You get to choose your coordinate system, and it's good to draw the x and y axes in your solution to make your coordinate system clear.
Maybe I am overlooking something simple but for some reason when I put in the inverse tangent of 0.1 on my calculator I get 0.099 and not 5.7. Do you know why this is?