Question
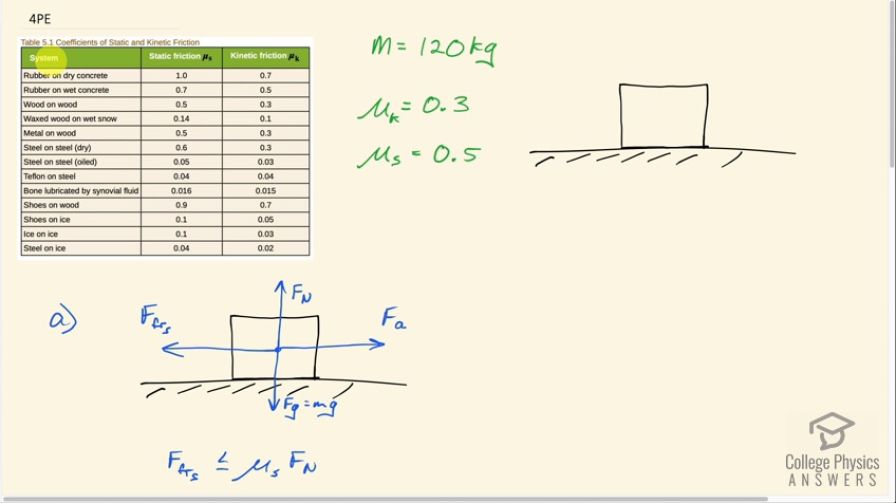
Suppose you have a 120-kg wooden crate resting on a wood floor. (a) What maximum force can you exert horizontally on the crate without moving it? (b) If you continue to exert this force once the crate starts to slip, what will the magnitude of its acceleration then be?
Final Answer
Solution video
OpenStax College Physics, Chapter 5, Problem 4 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. Crate made out of wood is resting on a floor also made out of wood and that tells us that when we look in table [5.1], we need to look at this wood-on-wood section to find the coefficient of static friction which is 0.5 and the coefficient of kinetic friction when it's sliding of 0.3. So we write those two pieces of information down. We are told the mass is 120 kilograms and then in part (a), we are asked what maximum force could we exert horizontally, what applied force could we apply such that the crate does not move? Now there's a normal force upwards exerted by the floor which is important because that is responsible in part for the friction force because the static friction force is this coefficient of static friction multiplied by this normal force and we also have the friction force opposing the applied force and we have gravity downwards. Now the friction force when it's in the static context is less than or equal to the coefficient of static friction multiplied by the normal force which means at its maximum, it's going to be equal to this product here. So we know that the normal force upwards is going to equal gravity downwards because there's no vertical acceleration and we also know that the applied force to the right is gonna equal the static friction force to the left because likewise there's no motion horizontally. So then we can make substitution's up here: we'll replace this maximum static friction force with the applied force—which is what we want to find— and we'll replace the normal force with mg—the force of gravity— and so then we have 0.5—coefficient of static friction— multiply by 120 kilograms times 9.80 meters per second squared which with one significant figure— since we have only one significant figure in our static friction coefficient— is 6 times 10 to the 2 newtons would be the maximum applied force you could apply without the crate moving. Part (b) says suppose it does start to slide anyway and you maintained the same applied force, what would the acceleration be? And it's gonna have acceleration because the friction force will change to the kinetic friction force now which is always less than the static friction force. So we have the force to the right— which is the applied force— minus this kinetic friction force to the left equals mass times acceleration—this is Newton's second law— and we divide both sides by m and we get acceleration then is this difference in these two forces divided by the mass. Now the kinetic friction force is the coefficient of kinetic friction multiplied by the same normal force as before—that being equal to gravity— and so then we plug in numbers here. So we have the acceleration then is 588 newtons which is the answer to part (a) but with no rounding because we don't want to have intermediate rounding error; we don't wanna round until we get to a final answer so I'm using this intermediate number of 588 newtons minus 0.3 which is the coefficient of kinetic friction times 120 kilograms times 9.80 meters per second squared divided by the mass giving us 2 meters per second squared acceleration.
