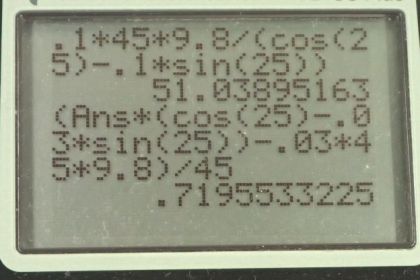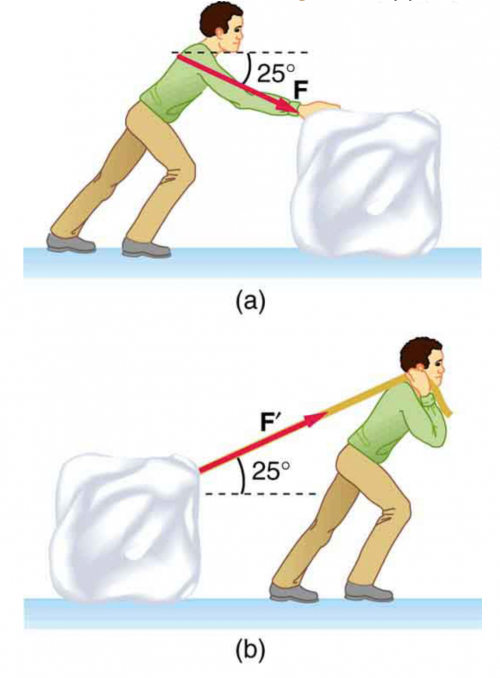
Solution video
OpenStax College Physics, Chapter 5, Problem 18 (Problems & Exercises)
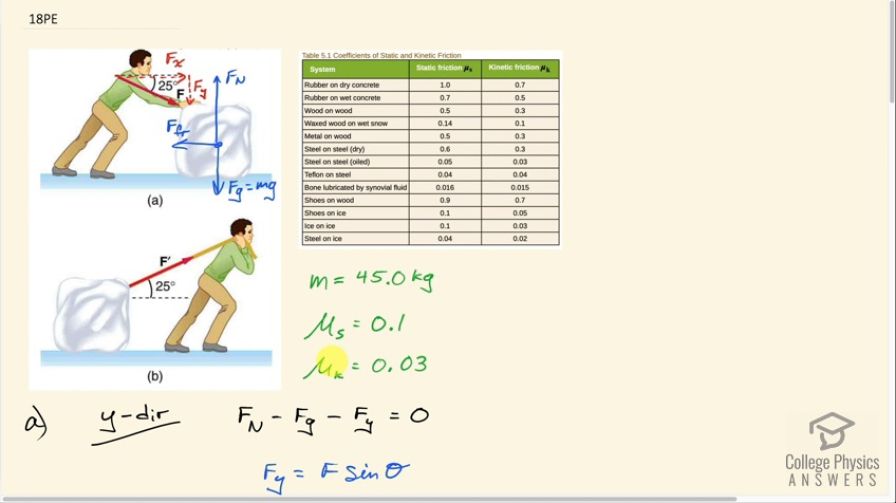
Calculator Screenshots
Comments
Why do given the solution as 50 if it comes out as 51. Are we suppose to be rounding to the nearest tenth?
Yes, exactly, we're rounding to one significant figure. This is due to the of the coefficient of static friction, which has only one significant figure. When multiplying by a number with one sig. fig., the answer gets only one sig. fig. also.
All the best,
Shaun
I'm still unclear on how rounding to the nearest tenth would take the answer from 51.03 down to 50 rather than 51.
Thanks for the question @George Fingerwalker,
If we're talking about part (a), then we're not talking about rounding to the nearest tenth. Only the acceleration in part (b) is rounded to the nearest tenth, to . In part (a) our calculation results in 51.03, as you mentioned. One of the factors by which we multiply to get 51.03 is the coefficient of friction, which is 0.1. The coefficient of friction has only one significant figure. The fact that the coefficient of friction is expressed with precision to the tenths place is not relevant, only its number of significant figures is relevant when multiplying. The result of multiplying several numbers needs to be rounded such that it has as many significant digits as the number with the fewest significant figures. The coefficient of friction has only one significant figure, so the result also needs to have only one significant figure. 51.03 expressed with only one significant figure is 50.
Hope this helps,
Shaun
The way they are teaching us about known coefficients is that they are actually exact numbers. All the constants, molar masses, are not affecting the # of sig figs in the answers my uni expects.
"Exact numbers have no uncertainty, and thus do not limit the number of significant figures in any calculation. We can regard an exact number as having an unlimited number of significant figures. "
Hi pansapinsa,
Thank you for the comment. I can totally understand how this is confusing. There is a place for the concept of "exact numbers" not affecting significant figures. In the formula for the circumference of a circle, for example, the factor 2 is exact. The factor 2 does not affect the number of significant figures in this calculation; it would not cause the answer to have only 1 significant figure, in other words. The factor 2 is not a measured value. When it comes to numbers such as the coefficient of friction, however, they are not exact, since they have been measured. The coefficient has been measured, and as such it has measurement error just like any other number that has been measured. Since this coefficient has only one significant figure, we must presume that this is the limit to its precision, otherwise it would be expressed as, for example, 0.1000, with some trailing zeros if it was more precise than 0.1.
It's possible that your uni is attempting to make the concept more simple for students by saying "ignore significant figures in values provided by the textbook". That approach doesn't pass scrutiny from the perspective of scientific integrity, but perhaps in their view there is a pedagogical benefit in attempting to bring attention to other physics concepts without becoming mired in error analysis. In your case, however, perhaps their simplification is paradoxically causing greater confusion.
Hope this helps, and good luck,
Shaun