Question
Show that the acceleration of any object down an incline where friction behaves simply (that is, where is . Note that the acceleration is independent of mass and reduces to the expression found in the previous problem when friction becomes negligibly small ().
Final Answer
see video for solution derivation.
Solution video
OpenStax College Physics, Chapter 5, Problem 9 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Video Transcript
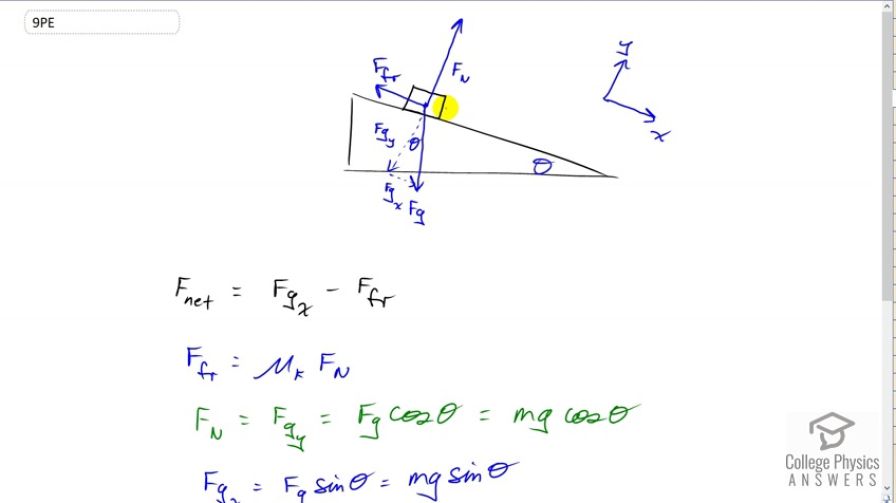
This is College Physics Answers with Shaun Dychko. We have an object on an incline which is inclined at an angle of theta and our job is to show that the acceleration of this object will be g times sin theta minus the coefficient of kinetic friction times cos theta. We’re also gonna notice that it is independent of mass, so mass doesn’t matter for the acceleration here. Now we show the three forces that are involved, this is a free body diagram. We have gravity straight down, the normal force is at a right angle to the incline and then we have friction moving up the incline. I’ve rotated the coordinate system just a little bit, it’s not exactly up and straight to the right, instead the x-axis is gonna go down the incline and the y-axis will go perpendicular to the incline. Sometimes, people leave the y and the x as they normally are and then write components that are parallel and perpendicular to the incline, that’s fine too. But I’ve rotated the coordinate system here. So we need to turn this force of gravity into components because the normal force is going to equal the component of gravity that is perpendicular to the incline surface or in the y direction here. The force to the right or down the incline is going to be the x component of gravity and then the force that is up the incline will be friction there. So we need to notice that that angle there, between the y component of gravity and gravity is theta. A good way to remember that that’s the case is to notice this triangle here and you can see that this is a right angle for sure, because this is the bottom of the incline and it’s straight to the right and this is gravity which is straight down, so this is a right angle. Which means this angle in here is going to be 90 minus theta because all three of these angles in the triangle have to add up to 180 and we have already accounted for 90 there, which means there’s 90 leftover for these two, so that means alpha is going to be 90 minus whatever the theta is. This angle that is here is also 90 because well we’ve defined it that way, we want this component here Fgy to be perpendicular to the incline surface and so that means that this angle here has to be 90 minus whatever alpha is. Then 90 minus whatever alpha is, 90 minus theta, is going to end up being 90 minus 90 plus theta which is theta. And so that’s a way to notice that this angle in blue, theta is equal to this angle of the incline. Alright. So the net force along the incline is going to be the component of gravity that is down the incline, Fgx minus the force of friction up the incline. The force of friction, because the box is moving, is going to be the coefficient of kinetic friction multiplied by the normal force Fn. The normal force is going to be equal to the component of gravity perpendicular to the incline or Fgy and Fgy is going to be Fg multiplied by cos theta because Fgy is the adjacent leg of this triangle. So that Fg is mg. We have Fgx is also Fg times sin theta because Fgx is the opposite leg of that triangle, and that is mg times sin theta then. we substitute all this into our net force formula, so we have Fgx is mg sin theta minus force of friction which is mu k times Fn but we’ll substitute for Fn as So mg cos theta, multiplied by the coefficient of kinetic friction, and all that equals mass times acceleration because that’s newtons’s second law, net force is always ma. Then we can divide both sides of this equation by m and then each term has the m cancelled there, and then the m cancels on the right side too and we’re left with a, multiplied by g sin theta minus mu k g cos theta. We can factor out the common factor g and we have a equals g times bracket sin theta minus mu k cos theta, which is what we want to show.