Question
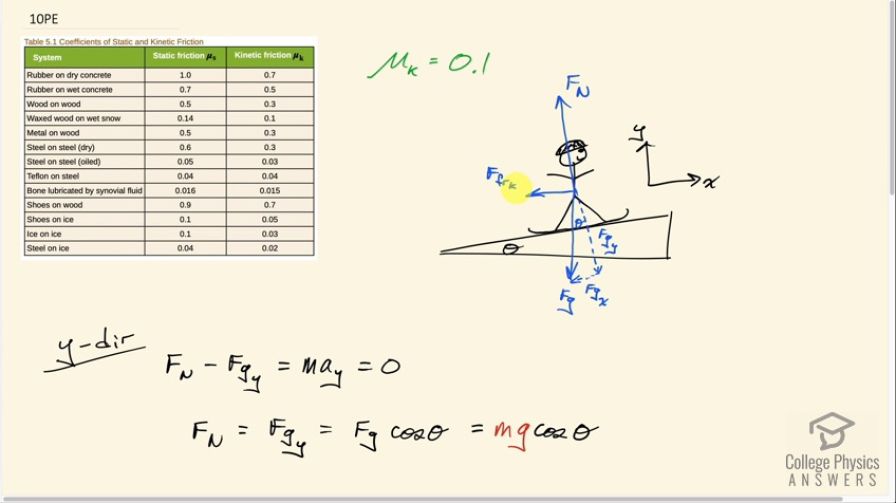
Calculate the deceleration of a snow boarder going up a , slope assuming the coefficient of friction for waxed wood on wet snow. The result of Exercise 5.9 may be useful, but be careful to consider the fact that the snow boarder is going uphill. Explicitly show how you follow the steps in Problem-Solving Strategies.
Final Answer
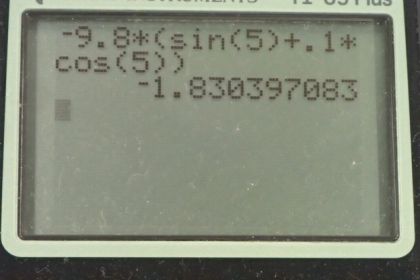
Note: In the video I made a rounding error in the final answer and mistakenly wrote . It should be .
Solution video
OpenStax College Physics, Chapter 5, Problem 10 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. The snowboarder is going up this incline and they will experience a friction force opposing their velocity and also there is a component of gravity which will also be opposing their velocity. And so we have defined our coordinate system so that the x-axis is positive up the slope and the y-axis is perpendicular to the slope and we have to look in table [5.1] for the coefficient of kinetic friction between waxed wood and wet snow which is 0.1 and our job is to figure out what is the deceleration of this snowboarder? So we'll consider the y-direction first because we need to know what this normal force is in order to calculate the friction force. So we can say that the normal force perpendicular away from the slope minus the component of gravity that is downwards and perpendicular to the slope equals the mass times the acceleration in the y-axis which is zero because they are not accelerating off the slope so then we can say that the normal force then equals the y-component of gravity and this angle in here is Θ and this gravity component here is the adjacent component in this right triangle so we use cosine of Θ multiplied by the hypotenuse which we know is mg to find this component perpendicular to the slope of gravity so the normal force then is this mg times cos Θ. Then we consider the x-direction which is the x-component of gravity which is to the left and so I put a minus sign in front of it and then also minus this friction force kinetic which is to the left equals mass times the acceleration which we have to find. So let's substitute for each of these terms here: we know that the kinetic friction force equals coefficient of kinetic friction multiplied by the normal force— and the normal force we found up here when we considered the y-direction— and we plug in mgcos Θ in place of the normal force. The x-component of gravity is going to be mg which is the hypotenuse of this right triangle multiplied by sin of this angle Θ because this is the opposite leg that we are finding now so we have mgsin Θ is the x-component of gravity. So we substitute for each of these terms here in red and then solve for the acceleration. We can divide both sides by m and so it's a factor that cancels in all the terms and we have the acceleration then is negative g— which I factored out among these two terms— times sin Θ plus kinetic friction coefficient times cos Θ. So we have negative 9.80 meters per second squared times sin of 5 degrees plus 0.1 times cos of 5 degrees which is negative 1.9 meters per second squared acceleration.