Question
A vertebra is subjected to a shearing force of 500 N. Find the shear deformation, taking the vertebra to be a cylinder 3.00 cm high and 4.00 cm in diameter.
Final Answer
Solution video
OpenStax College Physics, Chapter 5, Problem 37 (Problems & Exercises)
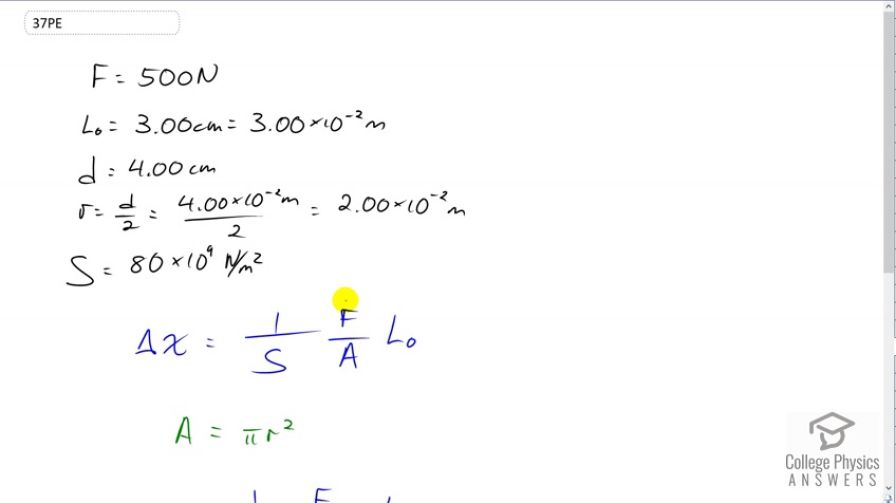
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. We're going to find the shear deformation of this vertebra using this formula, one divided by Shear Modulus, multiplied by the force applied, divided by the cross sectional area of the material, times its length. We start by writing down all the information we have. We're told that a force of 500 newtons is applied, a shear force, and the length of the vertebra is 3 centimeters which we convert into meters. The radius of the vertebra, 'cause we're suppose to model it as a cylinder, is going to be half the diameter. So the diameter is 4 centimeters, so we divide that by two and also convert the centimeters into meters. We have two times ten to the minus two meters is the radius. The Shear Modulus for bone is 80 times ten to the nine newtons per square meter. So this is our shear deformation formula, the amount that the cylinder will tip over so to speak, or like bend over. So, it'll bend so that it's like this after it's being pushed and it'll go this distance delta x. We need to find the area of this cross section there and since it's a circle, we can use pi r squared to find it. So we substitute pi r squared in place of a in the formula and then now we plug in numbers. So it's one over 80 times ten to the nine newtons per square meter Shear Modulus, times 500 newtons shear force divided by pi times two times ten to the minus two meters squared, times three times ten to the minus two meters length. This gives 1.5 times ten to the minus seven meters is going to be the amount that it has shear deformation, which is very small.
