Question
If an object is to rest on an incline without slipping, then friction must equal the component of the weight of the object parallel to the incline. This requires greater and greater friction for steeper slopes. Show that the maximum angle of an incline above the horizontal for which an object will not slide down is . You may use the result of the previous problem. Assume that and that static friction has reached its maximum value.
Final Answer
Please see the solution video.
Solution video
OpenStax College Physics, Chapter 5, Problem 12 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Video Transcript
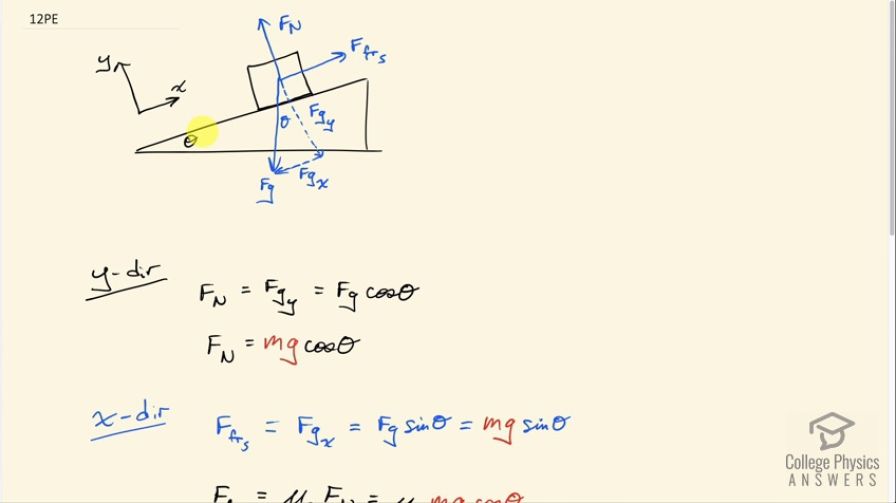
This is College Physics Answers with Shaun Dychko. This box is on an incline raised up an angle of Θ with respect to horizontal and there's some static friction force preventing it from sliding down the ramp and there's a component of gravity that's down the ramp and then this friction force and this gravity component have to be equal in order for there to be no acceleration or no movement. We have defined our axis so that the x-axis is positive up the slope and the y-axis is positive perpendicular to the slope. There's a normal force exerted by the slope and that normal force is going to be equal to the component of gravity which is perpendicular to the slope in the opposite direction. So we are gonna show that the angle Θ here, the maximum possible angle, will be the inverse tangent of the coefficient of static friction but let's step through the solution one step at a time. So in the y-direction, we'll consider this normal force upwards has to equal the component of gravity that is in the y-direction downwards in order for there to be no acceleration and this y-component of gravity is gravity multiplied by cos of this angle Θ here because this is the adjacent leg of this triangle and this is a right triangle. So we use F gcos Θ to find this adjacent leg and that is to say that the normal force then is mg because that's what gravity is—mass times gravitational field strength, g— times cos Θ. Okay that's useful because we are going to then talk about the x-direction which contains this friction force and the friction force depends on the normal force that we found when we considered the y-direction. So the friction force up the ramp has to equal the component of gravity that is down the ramp and that component of gravity is the opposite leg of this triangle and so we use sin Θ multiplied by the hypotenuse to get it and that hypotenuse is mg. We can also say that the static friction force is the coefficient of static friction multiplied by the normal force and that is μ s then times mgcos Θ that we substituted from here into there. So both this and this, both equal the static friction force and so we can equate them which we do here. So I put all of this in place of this here and we end up with μ smgcos Θ equals mgsin Θ. And then we can solve for the coefficient of static friction by dividing both sides by mgcos Θ and then we end up with μ s equals sin Θ over cos Θ and there's a trigonometric identity which says that when you have sin Θ divided by cos Θ that is the same as tangent Θ. So if we were to solve for Θ then we would take the inverse tangent of both sides and then we get our final answer: Θ is the inverse tangent of μ s.