Question
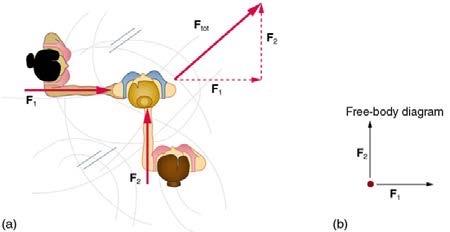
Consider the 65.0-kg ice skater being pushed by two others shown in Figure 5.19. (a) Find the direction and magnitude of FtotF_{tot}, the total force exerted on her by the others, given that the magnitudes F1F_1 and F2F_2 are 26.4 N and 18.6 N, respectively. (b) What is her initial acceleration if she is initially stationary and wearing steel-bladed skates that point in the direction of FtotF_{tot}? (c) What is her acceleration assuming she is already moving in the direction of FtotF_{tot}? (Remember that friction always acts in the direction opposite that of motion or attempted motion between surfaces in contact.)
<b>Figure 5.19</b> An ice skater being pushed by two other ice skaters.
Figure 5.19 An ice skater being pushed by two other ice skaters.
Question by OpenStax is licensed under CC BY 4.0
Final Answer

a) 32.3 N, 35.2∘ above positive x-axis32.3 \textrm{ N, } 35.2^\circ \textrm{ above positive x-axis}

b) 0.105 m/s2 in the direction of Ftot0.105 \textrm{ m/s}^2 \textrm{ in the direction of } F_{tot}

c) 0.301 m/s2 in the direction of Ftot0.301 \textrm{ m/s}^2 \textrm{ in the direction of } F_{tot}

Note: in some version of the textbook table 5.1 has a typo for the static friction of steel on ice. The static friction coefficient of 0.40 is incorrect. We expect a much lower coefficient for steel on ice since, from experience skating, the coefficient of static friction should be very small since it's really slippery standing on ice with skates on. 0.40 is a coefficient comparable to wood on wood (0.50), which is not slippery. Also, https://www.engineeringtoolbox.com/friction-coefficients-d_778.html gives a steel on ice static friction coefficient of 0.03, so I've presumed that the textbook author meant to write 0.04.

Solution video

OpenStax College Physics, Chapter 5, Problem 7 (Problems & Exercises)

OpenStax College Physics, Chapter 5, Problem 7 (PE) video thumbnail

In order to watch this solution you need to have a subscription.

Start free trial Log in
vote with a rating of votes with an average rating of .
Chevron left Prev
Next Chevron right

Calculator Screenshots

  • OpenStax College Physics, Chapter 5, Problem 7 (PE) calculator screenshot 1
  • OpenStax College Physics, Chapter 5, Problem 7 (PE) calculator screenshot 2
Video Transcript
This is College Physics Answers with Shaun Dychko. This skater in the middle is being pushed by two other skaters with the forces shown. We have 26.4 newtons to the right and 18.6 newtons upwards and this results in a total force exerted on the skater being F subscript tot for total. That is not the net force though because this question also asks us to consider friction. But the first thing we’re gonna do is figure out what this total force is and then in part b, we’ll say that friction is acting in the opposite direction to the total force on the object, or the opposite direction to what it’s motion is or would be. So the friction is going to be exactly in the opposite direction to Ftot. But let’s figure out what the Ftot is first. We’re conveniently given two forces that are at right angles with each other, so that means the x and y components of this total force are the forces given, F1 and F2. The Ftot is going to be the Pythagorean sum of F1 and F2, so that’s the square root of F1 squared plus F2 squared, and so that’s the square root of 26.4 newtons squared plus 18.6 newtons squared, giving us 32.3 newtons. The direction of this force theta is going to be the inverse tangent of the opposite divided by the adjacent, so it’s the inverse tangent of F2 over F1, so that’s the inverse tangent of 18.6 divided by 26.4 which is 35.2 degrees. So the total force vector is 32.3 newtons, 35.2 degrees above the positive x-axis. This is the positive x-axis here, and this angle is above that axis. And I wrote this little arrow here to say that what we’re talking about here is a vector, it’s not just a magnitude, it’s something that has a magnitude and a direction. Now in part b, we’re told that the skater is initially not moving which means the friction that’s in play here is the static friction. And so the net force is going to be the total force applied by the other skaters minus the friction force going in the opposite direction, and that friction force will be the coefficient of static friction which is why I have a letter s as a subscript there, multiplied by the normal force between the skater and the ice, and the normal force is going to equal the skater’s weight mg. So then we plug in numbers, so that’s 32.294 newtons which is the unrounded version of that to avoid intermediate rounding error, minus 0.04 which is the coefficient of static friction for steel on ice, you can find that in Table 5.1, multiplied by 65 kilograms times 9.8 newtons per kilogram, and that is 6.814 newtons. Now this net force also is mass times acceleration, that’s Newton’s second law. We’ll divide both sides by m, to get the acceleration is net force divided by m. So that’s 6.814 newtons divided by 65 kilograms which is 0.105 meters per second squared, and that’ll be in the direction of the total force applied by the other two skaters. Then in part c, it’s basically the same question because the same forces are applied except that the friction is now kinetic friction which is always less than static friction because in part c the skater is now moving. So the coefficient of kinetic friction for steel on ice is 0.02. That’s the number we plug in here, which is the same formula as up here but we have 0.02 instead of 0.04, so that works out to 19.554 newtons is the net force, and we divide that by 65 kilograms, that gives 0.301 meters per second squared, also in the direction of the total applied force.

Comments

On my table 5.1 Steele on ice for static friction is 0.40

Also, because she is initially stationary doesn't that mean she is not moving. Meaning that her acceleration would be zero?

Hi marievillafuerte, thanks for the question. It's possible there's a typo in your edition of the text. Perhaps you're using an older printed version? I'm seeing 0.04 in the pdf downloaded from https://openstax.org/details/books/college-physics-ap-courses. Also, we expect a much lower coefficient for steel on ice since, from experience skating, the coefficient of static friction should be very small since it's really slippery standing on ice with skates on. 0.40 is a coefficient comparable to wood on wood (0.50), which is not slippery. Also, https://www.engineeringtoolbox.com/friction-coefficients-d_778.html gives a steel on ice static friction coefficient of 0.03.

The skater moves as a result of being pushed by other skaters so, while she does begin from rest, she will be accelerated by the push from her two fellow skaters.

Hope that helps,

Shaun

Hi! i am also seeing that the text book provides a value of .4 rather than .04. I am using the most current edition of theOpenstax book found online. 

Hi alexgoble, thanks for the comment. 0.04 is definitely the best estimate for the coefficient of static friction for steel on ice. Some editions of the OpenStax text list 0.40 in table 5.1, as you've noticed. I'm using revision number "CPFAC-2015-002(03/17)-BW", which is the latest high res. version of the College Physics for AP Courses. Perhaps the regular "College Physics" text not intended for AP courses has an outdated table? In any case, 0.40 is an error, which can be verified by considering other data sources such as https://www.engineeringtoolbox.com/friction-coefficients-d_778.html. Thanks again for mentioning it though, since getting feedback from students with sharp eyes helps make College Physics Answers the best resource it can be.

How did you know about the static friction being 0.04? it doesn't say it on the problem.

Hi Rafmaster333, thank you for that question. It's a question shared by a couple of other students as well, so please just look at my replies to them above your comment. The short answer is that the textbook is incorrect to say 0.4, whereas an internet search says 0.04 is reasonable.

Hey guys, I am also seeing the Static Friction of steel on ice for 0.4. Which would make part B) 0 for acceleration. The formula is correct but and works for part C) it is just the wrong static friction.

Hi trwatkins, thank you for noticing this discrepancy between the textbook and the solution. Other students have noticed this also. I have made a note below the final answer to explain that the figure in the textbook is a typo, and the static friction coefficient should be 0.04.

I'm confused about part b. The answer appears to be Zero acceleration whereas the solution was different. I was hoping for some clarification. Thanks!

Hi bjappell, thank you for the comment. There is a net force on the skater in part (b) since the total force exerted exceeds the friction force, so the acceleration is not zero. If you could expand on what isn't clear I might be able to help better.
All the best,
Shaun

What I don't get is how we can use static friction when there's an acceleration. An acceleration means there's motion, and that makes me think to use kinetic friction. What point in time is the problem referring to if there's both an acceleration of the skater and static friction? Is it the first moment when she starts to move or just before then, or is it some point in time that inexplicably covers both of those moments? I don't get it.

Hi rrincones, thank you for the question. In part (b), where the skater is initially at rest, in which case static friction applies, we're considering only the brief instant when they're just beginning to accelerate. It might be helpful to think of it as an instantaneous force, which admittedly is an idealization. In part (c) the skater is already sliding, so then kinetic friction applies.
Careful with the idea of moving = kinetic friction. It's more accurate to say sliding = kinetic friction. Car tires normally have static friction (sometimes call "rolling friction" since it's not strictly static), unless the car is sliding, in which case there would be kinetic friction.
Hope this helps,
Shaun

I keep plugging the same thing in my calculator to find the Angle and it gives me a totally different answer. 0.557?

Hello, thank you for the question. A typical reason for an issue like this would be having your calculator in radian mode, which means it gives the answer is radians instead of degrees. In radians, the answer would be 0.61377, that's still different than 0.577. My suspicion is that your calculator is in radian mode, and something is being typed in slightly different... it's hard to say. When you figure out the issue please let us know.
All the best,
Shaun

No Q&As found for this question yet. How about you submit the first one?