Question
Ray tracing for a flat mirror shows that the image is located a distance behind the mirror equal to the distance of the object from the mirror. This is stated , since this is a negative image distance (it is a virtual image). (a) What is the focal length of a flat mirror? (b) What is its power?
Final Answer
- tends to infinity
- tends to zero
Solution video
OpenStax College Physics for AP® Courses, Chapter 25, Problem 60 (Problems & Exercises)
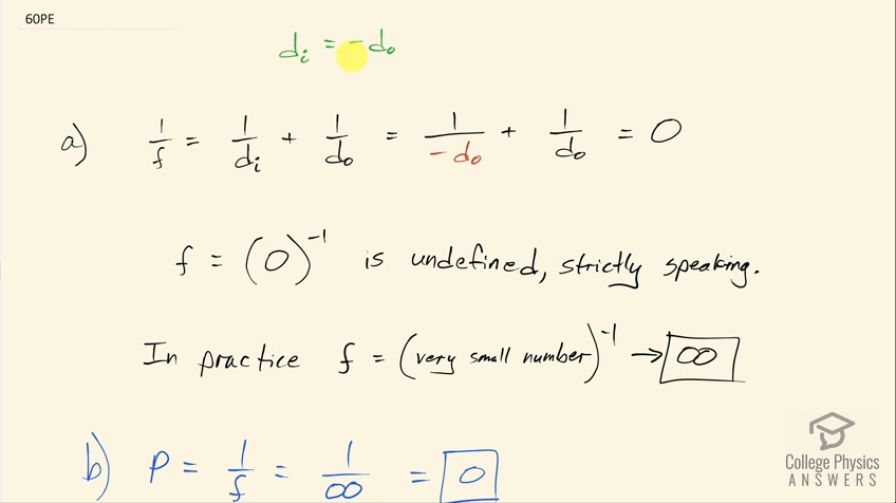
vote with a rating of
votes with an average rating of
.
Video Transcript
This is College Physics Answers with Shaun Dychko. A flat mirror has an image distance equal to the negative of the object distance so the image is the same magnitude distance from the mirror as the object is but just on the other side of the mirror; this is partly why mirrors make rooms seem bigger because it seems like things that are being reflected are far behind the mirror. Okay! So the question is what is the focal length of such a mirror? Well we have this equation for a mirror: 1 over focal length is 1 over image distance plus 1 over object distance, the image distance is the negative of the object distance so we can substitute that here and this works out to zero. Now if we raise both sides to the negative 1 to solve for f, strictly speaking from a math point of view, 0 to the negative 1 is undefined but in practice, you know, the mirror is not gonna be perfectly, perfectly flat, it's just gonna be very nearly so so we can consider this to be a very, very small number— not exactly zero— and you raise a very small number to the power of negative 1, you get a very large number and it approaches infinity as this very small number approaches zero so the focal length is approaching infinity. The power being the reciprocal of focal length is 1 over this infinity and that is... essentially tends towards zero.