Question
What is the speed of light in air? In crown glass?
Question by OpenStax is licensed under CC BY 4.0
Final Answer

vair=2.997×108 m/sv_{\textrm{air}} = 2.997\times 10^{8}\textrm{ m/s}
vcglass=1.97×108 m/sv_{\textrm{cglass}} = 1.97\times 10^{8}\textrm{ m/s}

Solution video

OpenStax College Physics for AP® Courses, Chapter 25, Problem 6 (Problems & Exercises)

OpenStax College Physics, Chapter 25, Problem 6 (PE) video thumbnail

In order to watch this solution you need to have a subscription.

Start free trial Log in
vote with a rating of votes with an average rating of .
Chevron left Prev
Select problem
Next Chevron right

Calculator Screenshots

  • OpenStax College Physics, Chapter 25, Problem 6 (PE) calculator screenshot 1
Video Transcript
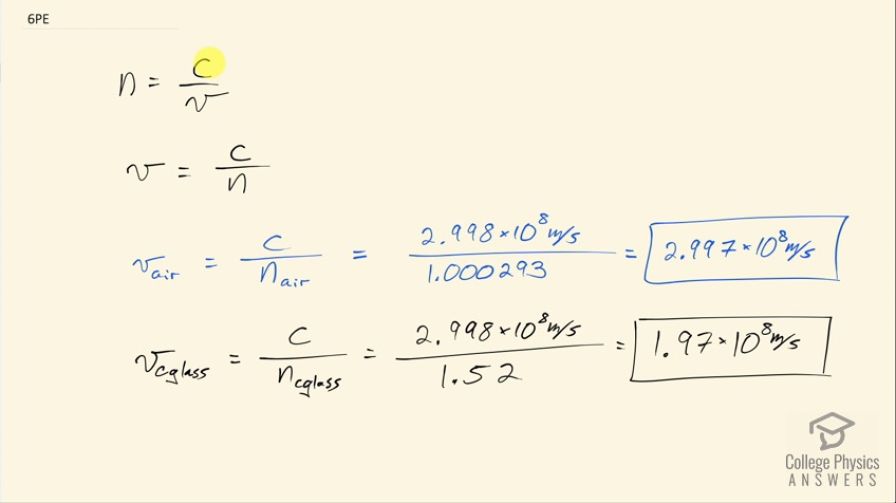
This is College Physics Answers with Shaun Dychko. We are going to figure out the speed of light in air and the speed of light in crown glass. So index of refraction is defined as the speed of light in a vacuum—c— divided by the speed of the light in some medium and we can solve for the speed of light in the medium by multiplying both sides by v over n so the speed of light in a medium is c over n. So in air, we have c divided by index of refraction of air and if we look that up in table [25.1], index of refraction in air is 1.000293 so we plug that in for n here and the speed of light is 2.998 times 10 to the 8 meters per second and we end up with 2.997 times 10 to the 8 meters per second is the speed of light in air. The speed of light in crown glass is the speed of light in a vacuum divided by the index of refraction of crown glass, which is 1.52. This works out to 1.97 times 10 to the 8 meters per second is the speed of light in crown glass.