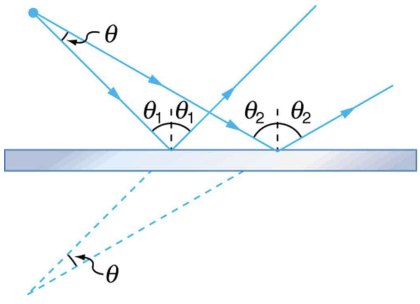
Question
A flat mirror is neither converging nor diverging. To prove this, consider two rays originating from the same point and diverging at an angle . Show that after striking a plane mirror, the angle between their directions remains .
Final Answer
Please see the solution video.
Solution video
OpenStax College Physics for AP® Courses, Chapter 25, Problem 4 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
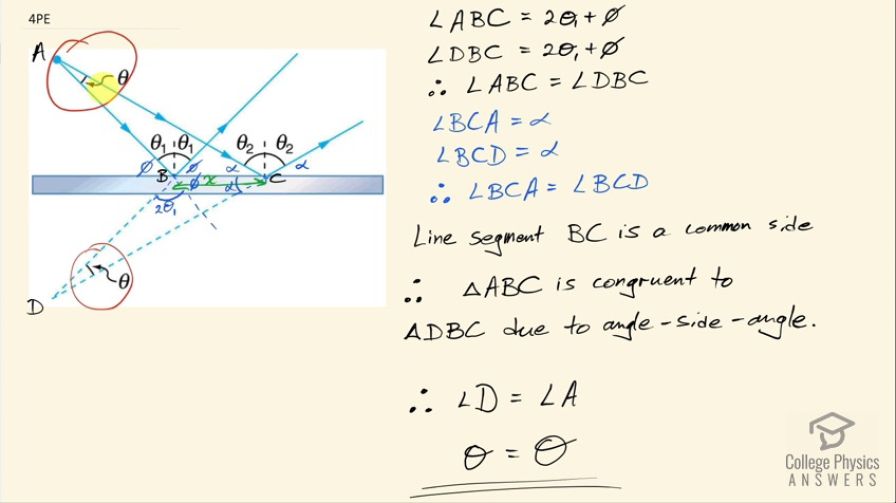
This is College Physics Answers with Shaun Dychko. We are going to show that this angle down here angle is Θ, the same as this angle up here. So we are going to look at this triangle which has points A, B and C and show that it's congruent to this triangle starting at point D, B and C. We can show that these triangles are congruent and that means that all the angles and all the side lengths are the same so then we can say that this angle here, which corresponds to this angle must be equal to it because the triangles are congruent. Okay! We are gonna use the angle-side-angle proof for congruency and so let's get started! We first can show that... we are gonna show that this angle here is the same as this angle here and first of all, we'll say that this portion here which goes from between this line and the extension of this line equals 2Θ 1 because these are opposite angles opposite sides of two crossed lines and then we need to look at this portion here between the mirror and this extended dotted line and it's Φ, which is the same as this angle here because these are opposite angles as well and since this angle plus Θ 1 is 90 then Θ 1 plus this other thing being also 90 these two must be equal as well and so... what we have here then is that this angle ABC angle ABC it equals 2Θ 1 plus Φ and then we are also showing that angle DBC is also 2Θ 1 from here plus Φ here and so they are equal to each other so angle ABC and DBC are both the same. Alright! Then we'll show that these angles here are the same, α and once we show that, we'll be able to use angle-side-angle as our proof of congruency because the triangles share this common side between points B and C. So angle BCA—we'll just call it α— and BCD is also α because α and Θ 2 make 90 and here we also have Θ 2 plus some other angle which equals... totals 90 and so these two angles must be the same and if these two angles are the same and this angle equals this angle because they are opposite of two crossed lines— the plane of the mirror and this line here— and so there we have these two angles are the same so angle BCA is equal to angle BCD since they are both α. Okay! And then the side between these angles is a common side so it's equal in both triangles and therefore these triangles are congruent. So ABC is congruent to triangle DBC and with that being true, angle D must equal angle A in which case it is Θ. So there we go!