Question
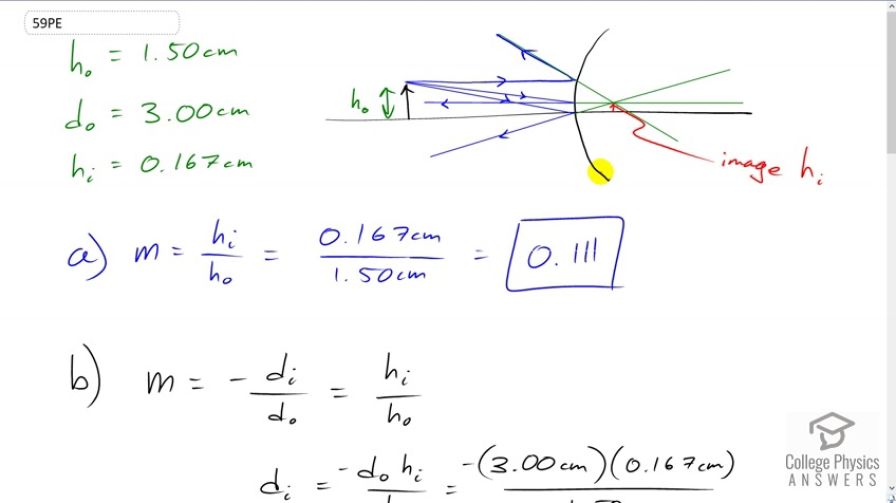
An object 1.50 cm high is held 3.00 cm from a person’s cornea, and its reflected image is measured to be 0.167 cm high. (a) What is the magnification? (b) Where is the image? (c) Find the radius of curvature of the convex mirror formed by the cornea. (Note that this technique is used by optometrists to measure the curvature of the cornea for contact lens fitting. The instrument used is called a keratometer, or curve measurer.)
Final Answer
- behind the cornea.
Solution video
OpenStax College Physics for AP® Courses, Chapter 25, Problem 59 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. Here's a ray diagram for the scenario where this curve is the cornea. That's the outer part of the eye, the non-white part. It consists of the iris and then the pupil in the middle. And, an optometrist does this very experiment in order to figure out what is the curvature of the cornea in order to fit contact lenses using an instrument called a keratometer. So, we have this object here, at some known distance, some known object distance and we know the object height and the image height as well. And so, I've drawn a ray that's parallel to the principal axis and then it gets reflected from this convex mirror. Such that this ray appears to have come from the focal point. And then, another ray is incident towards the focal point and then gets reflected parallel to the principal axis. And then, another ray hits the mirror at the principal axis and then gets reflected at the same angle as the incident angle. And so, when extending these three lines back, they converge at the point of the image corresponding to the point of the object where it started. And so, the image is here, and we can see that it's upright and smaller. So, we're expecting a magnification that is less than one and positive because the image and the object are both pointing in the same direction. So, magnification is image height divided by object height. And so, that's 0.167 centimeters divided by 1.5 centimeters, which is a magnification of 0.111. And then in part B, we're asked to find the image distance, so that is this distance here. And, we're expecting a negative answer because this is a virtual image because it's behind the mirror, so there's no light rays that pass through this point and for that reason it's called a virtual image. And, image distances are negative for virtual images, so let's see what we get here. So, we have magnification is negative of image distance over object distance and it also is image height divided by object height. And, we know these two things, and we can... we also know object distance, so we multiply both sides by that and we'll solve for image distance. And, multiply both sides by negative as well and you get image distance is negative object distance times image height divided by object height. So, that's negative of three centimeters times 0.167 centimeters image height divided by 1.5 centimeters object height, giving an image distance of negative 0.334 centimeters. So, that's 0.334 centimeters behind the cornea. And then, we're asked to find the radius of curvature of this convex mirror. So, because this is a diverging mirror, we expect its focal length to be negative and therefore, its radius of curvature will also be negative. So, radius of curvature over two is the focal length. And so, multiply both sides by two to solve for R. So, radius of curvature is two times the focal length. So then, we need to figure out what the focal length is. So, the thin lens equation also applies to mirrors. One over focal length equals one over image distance plus one over object distance. And then, we raise both sides to the exponent negative one and we get this formula for focal length, which we substitute in for F in our formula for the radius of curvature. So, the radius of curvature is two times one over image distance plus one over object distance all to the negative one. And, so that is two times one over negative 0.334 centimeters that we calculated in part B plus one over three centimeters object distance all to the negative one, giving negative 0.752 centimeters is the radius of curvature.
