Question
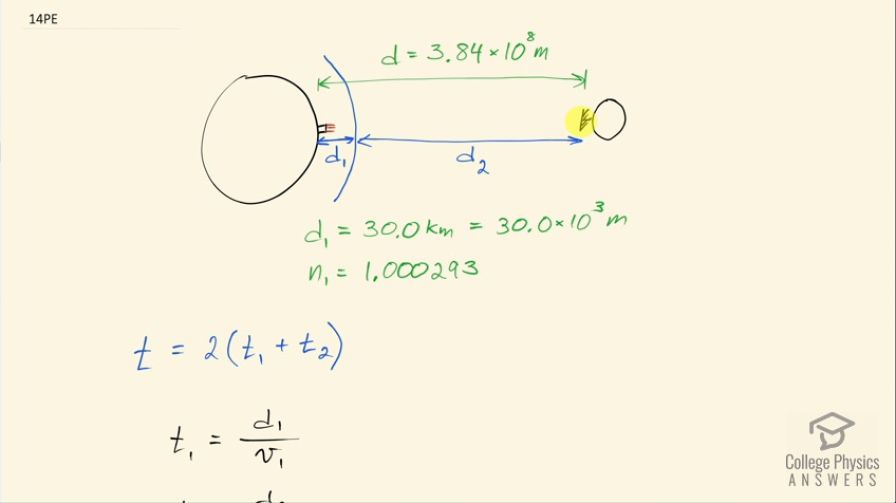
On the Moon’s surface, lunar astronauts placed a corner reflector, off which a laser beam is periodically reflected. The distance to the Moon is calculated from the round-trip time. What percent correction is needed to account for the delay in time due to the slowing of light in Earth’s atmosphere? Assume the distance to the Moon is precisely , and Earth's atmosphere (which varies in density with altitude) is equivalent to a layer 30.0 km thick with a constant index of refraction .
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 25, Problem 14 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Video Transcript
This is College Physics Answers with Shaun Dychko. A laser is shining from the Earth onto a mirror mounted on the Moon by some astronauts and then the light is bouncing back to the Earth and being detected sometime later and the time it takes for the light to make this round trip is being measured and used to figure out the distance to the Moon. Well let's suppose that we know the exact distance to the Moon is 3.84 times 10 to the 8 meters and we know that the height of the atmosphere is 30.0 kilometers, which is 30.0 times 10 to the 3 meters and the atmosphere has an index of refraction, n 1 which is 1.000293 if the people measuring this time make the assumption that the speed of light goes at the speed c, which is the speed of light in a vacuum, they will not be accounting for this portion of the trip when light is actually going slower through the air and so we want to figure out what percent error needs to be taken into account to account for this slowness through the air? Okay! So the total time it takes the light to make a round trip is 2 times the time it takes to get through the air, which we'll call t 1, plus the time it takes to get from the top of the atmosphere through empty space, which is a vacuum to the Moon. So t 1 is this distance d 1— the thickness of the atmosphere—divided by the speed of light through the air v 1 and time two is this distance from the top of the atmosphere to the Moon divided by the speed of light in a vacuum and so we can replace each of the time terms with those fractions and the percent error then is going to be the difference in time between this versus what would be measured if the light went at the speed c the entire time divided by the time at speed c times 100 percent. So the time if there's no atmosphere affecting anything the time at the speed of light would be 2 times the distance from the Earth to the Moon divided by c so we can replace a whole bunch of things in this step here. So t c is replaced by 2 times the Earth-Moon distance divided by c— this term, and down here as well— and this time here is what's actually going to be measured and it's 2 times the atmosphere thickness divided by the speed through the atmosphere plus the top of atmosphere to the Moon distance divided by c. Now d 2 is the total distance from the Earth to the Moon minus the thickness of the atmosphere so we can replace d 2 with that and we do that here. And then multiply both terms by 2 and then separate this into 2 terms by dividing both terms in the numerator by c. So we have 2d 1 over v 1 plus 2d over c minus 2d 1 over c minus 2d over c all over 2d over c times 100 percent and these are equal and opposite signs so they make zero and we can factor out the 2d 1 from this term and this term so we have 2d 1 times 1 over v 1 minus 1 over c all over 2d over c. And dividing by this fraction 2d over c is the same as multiplying by c over 2d and so that's how we get this line here— 2d 1c over 2d times 1 over v 1 minus 1 over c times 100 percent— the 2's cancel and then we want to replace v 1 with a different expression in terms of things that we know such as the index of refraction of the air. So the index of refraction of the air is c divided by the speed of light through the air and we can solve for v 1 by multiplying both sides by v 1 over n 1. So v 1 is c over n 1 and this term is a reciprocal of v 1 so we replace it with the flipped version of that fraction—n 1 over c— and now c is a common factor in the denominator and when it factors out, it will cancel with this c and so we have d 1 over d times n 1 minus 1 times 100 percent is going to be our answer. So that's 30.0 times 10 to the 3 meters— thickness of the atmosphere— divided by 3.84 times 10 to the 8 meters— exact distance from the Earth to the Moon— multiplied by 1.000293 minus 1 times 100 percent, this works out to 2.29 times 10 to the minus 6 percent is the percent error or the percent difference you would have to account for to get the correct measurement and this small percentage is indicative of the small thickness of the atmosphere.