Question
A parallel beam of light containing orange (610 nm) and violet (410 nm) wavelengths goes from fused quartz to water, striking the surface between them at a incident angle. What is the angle between the two colors in water?
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 25, Problem 32 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
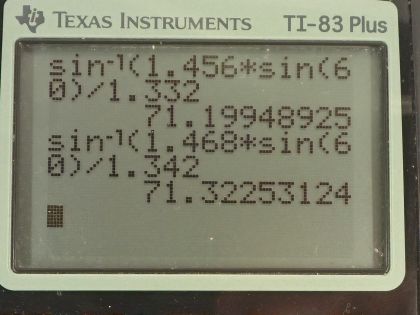
This is College Physics Answers with Shaun Dychko. A beam of light that consists of orange and purple mixed together is incident on this interface between fused quartz initially and then going to water as the second medium and it's going to refract away from the normal but the colors are going to refract different amounts because the index of refraction of the initial and final media are different for the different colors and that's the meaning of dispersion: different indexes of refraction for different colors. So the initial angle for each color is the same— they are both incident at 60.0 degrees so Θ 1 is 60.0 for both colors— but the first index of refraction for orange— this is meant to be the letter o not the number 0— the index of refraction for orange and for the first medium is 1.456, which we find in table [25.2] so we are dealing with fused quartz, which is this bottom row here and orange has an index of refraction of 1.456 and for water, the color orange has an index of refraction of 1.332 so that's where these two numbers come from and then fused quartz for violet is 1.468 and then for water, it's 1.342 so that's where these numbers come from. So we apply Snell's law separately for each color using their respective indices of refraction. So that means n 2 for orange times sin Θ 2 for orange equals n 1o times sin Θ 1, which does not need a subscript o nor v since both colors are incident at the same angle Θ 1 and our goal in the end here is to find the difference in angles of refraction so we are gonna subtract these two angles as our last step. So sin Θ 2o—this angle here— is going to be n 1o times sin Θ 1 over n 2o and then we take the inverse sin of both sides and then we end up with sin Θ 2o is the inverse sin of n 1o sin Θ 1 over n 2o. So it's the inverse sin of 1.456— index of refraction of orange infused quartz— times sin of 60.0 degrees divided by the index of refraction of orange in water—1.332— and this gives us an angle of 71.1995 degrees is this angle in the water between the orange and this normal. sin Θ 2 for violet, we would follow the same process and so let us just jump in at the last step here, which is inverse sin of the index of refraction for violet in the first medium— that being fused quartz, which is 1.468— times sin of that incident angle of 60.0 degrees divided by the index of refraction of violet in the second medium, which is water which is 1.342 and this gives us an angle for violet in water of 71.3225 degrees. And then we take the difference between these two angles, 0.123 degrees is the difference in the angles of refraction for these two colors.