Question
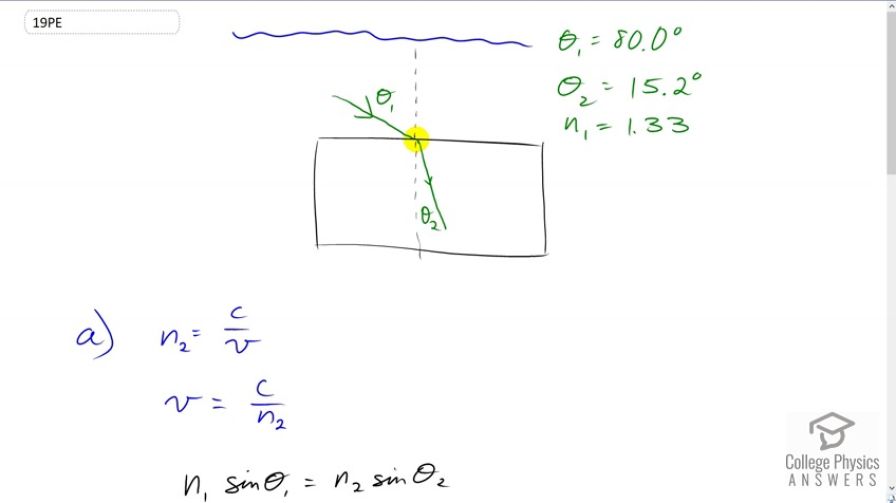
Light traveling from water to a gemstone strikes the surface at an angle of and has an angle of refraction of . (a) What is the speed of light in the gemstone? (b) What is unreasonable about this result? (c) Which assumptions are unreasonable or inconsistent?
Final Answer
- The speed of light is too slow. In diamond, which has the slowest light among materials in table 25.1, the speed of light is
- Either the angle of refraction is too small or the incident angle is too large.
Solution video
OpenStax College Physics for AP® Courses, Chapter 25, Problem 19 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. We have light traveling through water at an incident angle of 80 degrees and then it hits this gemstone and has an angle of refraction of 15.2 degrees. And our question is, what is the speed of light in this gem stone? Now, to figure that out, we need to know what its index of refraction is because the index of refraction is going to be the speed of light in a vacuum divided by speed of light in the gem stone. So, we'll multiply both sides here by V over N two, and we see that the speed that we want to find is going to be speed of the light in the vacuum divided by the index of refraction of the gem stone. Now, we can use Snell's law to figure out what N two is because we know what N one is, that's the index of refraction of water, which is 1.33. And, we'll solve this for N two by dividing both sides by sine theta two. So, the index of refraction of the gem stone equals the index of refraction water times sine of the incident angle divided by sine of the angle of refraction. So, V then is going to be C divided by this. And, instead of dividing a fraction by a fraction, I'm going to multiply by the reciprocal of N two. So, we have C multiplied by the reciprocal of this. So, that's C times sine theta two over N one sine theta one. So, the speed of light in the gem stone is going to be three times ten to the height meters per second times sine of 15.2 degrees divided by 1.33 times sine of 80 degrees, which is 6.01 times ten to the seven meters per second. Now, that number is not really reasonable because if you consider in table 25.1 the material with the highest index of refraction and therefore the slowest speed of light within it, that is diamond and that's going to have an index of refraction of 2.419, and when you divide that in to the speed of light in a vacuum, it works out to 1.24 times ten to the eight meters per second is the speed of light in diamond, which is an order of magnitude greater than what we calculated here. So, this number is unreasonably small. So, we can examine this to figure out what the problem must have been either we can reduce this number to make the fraction bigger and the speed bigger or we can increase this number. So, either the angle of incidence that has been given to us is too large and it should be smaller or the angle of refraction should be larger and what we're given has been too small. And, there we go.
