Question
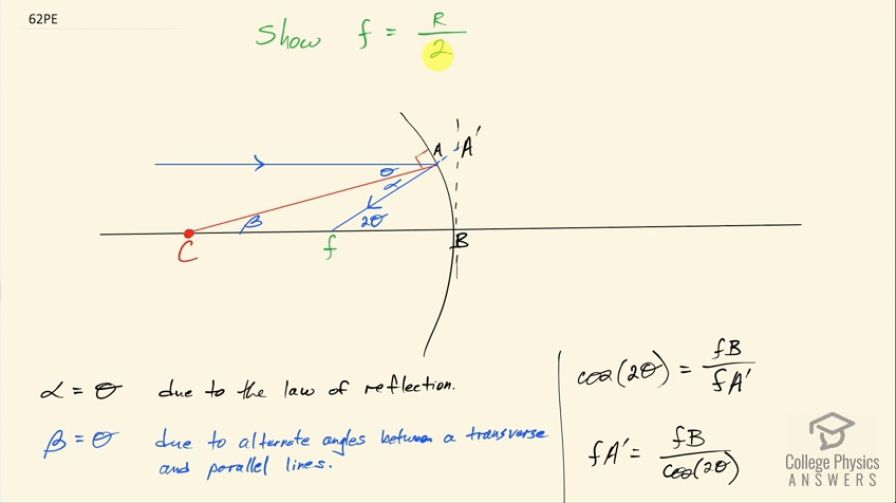
Use the law of reflection to prove that the focal length of a mirror is half its radius of curvature. That is, prove that . Note this is true for a spherical mirror only if its diameter is small compared with its radius of curvature.
Final Answer
Please see the solution video.
Solution video
OpenStax College Physics for AP® Courses, Chapter 25, Problem 62 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Video Transcript
This is College Physics Answers with Shaun Dychko. Our job in this question is to show that focal length for a mirror is its radius of curvature divided by 2 and let's be more precise here by saying that this is not a very precise relation, it's an approximation to say that the focal length is approximately equal to the radius of curvature over 2 and we'll have to make some approximations in our work here in order to establish this. So we have an incident ray that is parallel to the principal axis drawn in black and it's gonna reflect off the mirror through the focal length or through the focal point and this is by definition so an incident ray parallel to the principal axis reflects through the focal point. We have this line drawn in red, which is connecting from the mirror to the center of curvature and this line is a radius, the mirror being, you know, part of a circle one can imagine... this being the center of the circle and the radius tangent angle is always 90 degrees and so that's why we have this right angle there and so this angle Θ then is between the incident ray and the perpendicular to the surface and so that's the incident angle Θ and then this angle here is the angle of reflection between this perpendicular to the mirror in red and this blue line here going through the focal point. Now the law of reflection says that the reflected angle is the same as the incident angle and so we know that α and Θ are equal. Now because this incident ray we have designed to be parallel to this principal axis, we can say that this red line is a transverse between two parallel lines in which case alternate angles on either side of the transverse are equal— these are interior alternate angles— so that means β equals Θ. So Θ equals α and Θ equals β which means that α and β are also Θ— they are equal as well— and this triangle from point C to A to f is isoceles. Okay! So this line equals this line and this is the triangle I was just speaking of. Okay! Good! And then the next thing to talk about is this triangle... (oops) let's talk about a different triangle here... let's talk about this triangle. Now when you are doing your ray-tracing diagrams, strictly speaking, you are meant to make your lines go all the way to this vertical dotted line and if you reflect off of that then your ray-tracing diagrams will work out nicely because the assumption is always that the size of the mirror is very small in comparison to the radius of curvature so in fact the mirror is practically flat in that case and so these drawings such as the one I have here showing this curvature, it's not true to life here... this is just a way of illustrating the fact that we have a curved mirror but the curvature is... this greatly exaggerates the curvature the way I have drawn it and so let's consider this triangle here— it's a right triangle— and we are gonna have cosine 2 Θ is this angle here... oh, this angle is 2Θ because α and Θ are the same due to the law of reflection and this blue line is a transverse between these parallel lines as well and so this equals this total here so that's why that's 2Θ cos of that is equal to the adjacent, which is between points f and B and this points from f to A prime; I put A prime on this vertical dotted line and point A is on the mirror so we are talking about A prime here and so fA prime then is fB over cos 2Θ, you can multiply both sides by fA prime and divide both sides by cos 2Θ and then for small angles, cos 2Θ is essentially 1; if you have a graph of cosine of, you know, 2Θ or whatever Θ the graph is like this and for angles that are very, very close to zero, you are essentially at the maximum value for cosine, which is 1. And such is the case here... we have to assume that this angle is very small and that the mirror is small in comparison to its radius of curvature in other words. So that means that fA prime essentially equals fB because this denominator is 1 and fA is pretty much the same as fA prime, this little portion here is negligibly small because again this mirror is small compared to its radius of curvature and I have drawn the curvature way too big. Okay! Good! So now we have the distance from C to B is R— by definition because this is the center of curvature so this distance is the radius— we have established that fB is basically the same as fA—that's what we figured out here— and so we have this distance R being broken up into two equal parts one of which is of length of the focal length. So this distance CB is R and fB is the same as fA— fB is the same as fA— and Cf is basically the same as fA— Cf is the same as fA— that's the isoceles triangle business, you know, given that these angles are the same— this side is the same as that side and if this side is the same as that side then Cf is equal to fB— and that means CB—this radius side—is 2 times one of these segments so CB is 2 times this segment say from f to B and so we can say fB is CB over 2 and CB is R so divided by 2 and fB is f and so we have a relation that f is approximately equal to half the radius of curvature.