Question
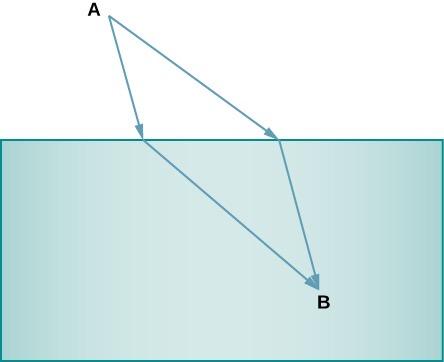
Referring to Figure 25.57: two different potential paths from point A to point B are shown. Point A is in the air, and point B is in water. For which of these paths (upper or lower) would light travel from point A to point B faster? Which of the paths more accurately represents how a light ray would travel from point A to point B? Explain.
Final Answer
upper path.
Solution video
OpenStax College Physics for AP® Courses, Chapter 25, Problem 7 (Test Prep for AP® Courses)

vote with a rating of
votes with an average rating of
.
Video Transcript
This is College Physics Answers with Shaun Dychko. A Light Ray is traveling from air into water. So it goes from a medium of index of refraction of 1.00 to a medium with an index of refraction of 1.33 and we can use Snell's Law to verify that the angle of refraction Theta two has to be less than the angle of incidence Theta One and so that means this upper path is what the light is going to follow. So n1 sine Theta One equals n2 sine Theta Two. That's Snell's Law and we can solve for Theta two by dividing both sides by n2 and then we get sine Theta Two is n1 sine Theta One over n2 and now since n2 is greater than n1. So the refraction of water is greater than the initial index of refraction in air. That means that this is going to be greater sorry, this is going to be less than sine Theta One because sine Theta One is getting multiplied by a fraction is less than one because the denominator is bigger than the numerator there. So sine Theta Two is going to be less than sine Theta One since the denominator n2 is greater than the numerator factor n1 and with sine Theta two being less than sine Theta One that means Theta Two is less than Theta One and that's true for this upper path.